La synthèse des éléments

Introduire un peu formation des éléments etc. + parler de hoyle

Au début des années 1940, une hypothèse à l'étude est l'abondance relative des atomes dans l'Univers s'explique par un équilibre thermique rapide ayant eu lieu à une température $T$ qui aurait gelé les proportions des différentes espèces. Très approximativement, ces proportions devraient suivre une distribution de type Maxwell-Boltzmann $n \propto e^{-E/(k_B T)}$ où $E$ est leur énergie nucléaire de liaison. L'énergie de liaison augmentant linéairement avec la masse atomique, l'abondance des espèces devrait décroitre exponentiellement avec celle-ci. Mais ce n'est pas ce qu'on observe : au lieu de cela, l'abondance des espèces lourdes est à peu près constante. L'idée d'un équilibre thermique rapide est donc rejetée.

Afficher/Masquer

Logarithme de l'abondance relative des éléments et fit pour une distribution de boltzmann selon les énergies de liaison (gnuplot)

Un fit naif est réalisé sur la portion $0 \leq A \leq 80$ de la courbe . La meilleure correspondance est atteinte pour une température d'équilibre de l'ordre de $10^{12}$ K, mais cela est incohérent avec le résultat pour des valeurs de $A$ supérieures (à partir d'environ 100-120) où la pente s'annulle inexplicablement. TODO: vrai fit avec

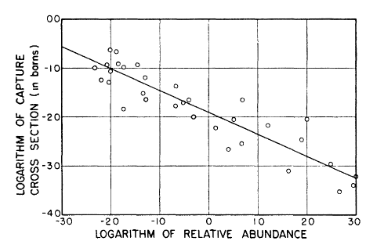
A partir de 1946, Gamow propose (G. Gamow  1946) , en réponse à l'échec de cette explication, une autre théorie de formation des éléments basée sur un processus hors équilibre qu'il justifie par l'expansion rapide de l'Univers. Il montre dans le cadre du modèle d'Einstein-de Sitter que l'Univers se serait trouvé dans un état de densité suffisant pour autoriser des réactions nucléaires pendant un temps très court, vers ses tous premiers instants, pendant lequel un équilibre n'aurait pu être atteint. Gamow suggère alors un mécanisme, après qu'il ait remarqué une forte corrélation entre les sections efficaces de capture de neutrons par des noyaux et leur abondance :

1. Dans ses premiers instants, l'Univers se trouve dans un état où il est dominé par des neutrons
2. Les neutrons s'agglomèrent très vite par capture neutronique pour former successivement des éléments contenant de plus en plus de nucléons. Ceci doit se faire très rapidement étant donné le temps de demie-vie du neutron qui se désintègre en environ 1000 s : sinon, tous les neutrons seraient devenus des protons avant de s'agglomérer.
3. Ces éléments lourds qui se forment se stabilisent par radioactivité $\beta^-$ (leurs neutrons deviennent des protons) donnant les atomes stables dont on mesure aujourd'hui l'abondance.
4. Les neutrons finissent par se désintégrer, et par ailleurs l'expansion ralentit la chaine d'agglomérations.

Corrélation entre section efficace de capture neutronique et abondance

Ce graphe tiré de "The theory of origin and relative abundances distribution of the elements" (Ralph A. Alpher, Robert C. Herman  1950) montre la corrélation entre abondance relative d'une noyau $_{Z}^{A}X$ et la section efficace de capture neutronique $_{Z}^{A}X+n \rightarrow _{Z}^{A+1}X$. Ceci montre que les éléments les moins abondants sont les plus susceptibles de capturer un neutron, ce qui suggère un mécanisme comme celui proposé par Gamow.

L'univers jeune dominé par les photons

En 1948, Gamow, Alpher et Herman publient de nombreux papiers dans le cadre de cette théorie (R. A. Alpher, H. Bethe et al.  1948) . Ils comprennent que pour expliquer la présence importante d'hydrogène, il est nécessaire que les protons issus de la désintégration des neutrons libres n'aient pas tous formé avec eux du deutéron (noyau constitué d'un proton et d'un neutron). Ils proposent alors que la formation du deutéron soit en fait un équilibre : \begin{equation} n+p \rightleftharpoons d+\gamma \end{equation} Cet équilibre maintient la quantité de neutrons en empêchant leur désintégration (les neutrons libres réagissent pour former du deutéron dans lequel ils sont stables puis sont libérés à nouveau très vite par rapport à leur temps de demi-vie). Pour que la réaction inverse (et donc l'équilibre) soit possible, il faut que l'Univers contienne de l'énergie sous forme de photons à un niveau comparable à l'énergie de dissociation du deutéron, ce qui correspond d'après les trois physiciens à un rayonnement d'une température de l'ordre de ($10^9$ K). Avec l'expansion, l'énergie des photons diminue jusqu'à ce que la réaction inverse soit impossible. Ils comprennent alors que l'Univers devait être très chaud, et que la densité d'énergie de radiation $\sim \sigma T^4/c$ était très supérieure à la densité d'énergie de la matière non relativiste. Ceci a plusieurs implications. D'abord, d'après les équations de Friedmann, cela signifie que l'expansion était gouvernée par le rayonnement. De plus, ce rayonnement qui a du refroidir avec l'expansion devrait toujours exister, et en connaissant sa température à un instant donné (ici celui où les photons cessent de contribuer à l'équilibre du deutéron), il est possible d'en déduire la valeur actuelle. Ce sont Alpher et Herman qui proposent ainsi pour la première fois l'existence de ce qui est aujourd'hui appelé fond diffus cosmologique ("CMB" en anglais pour cosmic microwave background); Ils établissent plusieurs estimations de sa température variant entre quelques Kelvins et quelques dizaines de Kelvins

En 1950, des travaux menés par Enrico Fermi et Anthony Turkevich portant sur les réactions nucléaires entre éléments de taille $A \leq 7$ améliorent de façon significative la nature des processus en jeu dans ce modèle et de leur section efficace. Il apparait alors que ces réactions ne peuvent expliquer la formation d'éléments plus lourds que le béryllium (TODO: $A = 5,8$ posent pb).

Parallèlement, Hayashi suggère que des mécanismes (électrofaibles|fort?) ont instauré un équilibre qui a imposé le rapport $p/n$ avant la nucléosynthèse, en contradiction avec l'hypothèse initiale de Gamow d'un état initial constitué uniquement de neutrons dont la désintégration serait la seule source de protons. \begin{equation} p+e^- \rightleftharpoons n+\nu_e \end{equation} Ainsi, Hayashi trouve un ratio protons/neutrons $n_p/n_n \sim 4$ au lieu de $1/7$ environ comme estimé par Gamow, Alpher et Herman en ne considérant que la désintégration des neutrons. Or, cette valeur ne permet pas de rendre compte de l'abondance observée des éléments pour une nucléosynthèse par capture neutronique successive. Puisque la détermination de ce ratio $p/n$ est cruciale pour déterminer la vraisemblance de la nucléosynthèse par capture neutronique, Alpher, Herman et Follin publient un papier en 1953 visant à estimer l'état initial de l'Univers avant la nucléosynthèse (Ralph A. Alpher, James W. Follin et al.  1953) , selon les développements théoriques à leur disposition (qui leur permettent de décrire assez précisemment les phénomènes en jeu jusqu'à une température d'environ 100 MeV ~ $10^{12}$ K) et en étudiant la dépendance en certaines valeurs expérimentales mal connues (par exemple, le temps de demie-vie du neutron). Ils estiment que $p/n$ est compris entre $4,5$ et $6$, ce qui remet en effet en cause la nucléosynthèse par capture neutronique. Ce papier constitue cependant une base importante en tant que description alors la plus détaillée des premiers instants d'un big bang chaud.

Récapitulatif des différentes étapes du Big Bang selon Alpher-Hermann-Follin 1953

Grâce aux travaux d'Alpher, Gamow et Herman, on sait décrire dès le début des années 1950 un Univers en évolution de type Big Bang dans son jeune âge. On sait que dans un contexte de refroidissement rapide depuis des températures très élevées des éléments légers peuvent se former (jusqu'à $A = 5$) par le biais d'un réseau de réactions nucléaires, mais pas des éléments plus lourds a priori. On sait par ailleurs qu'il doit subsister, d'après ce modèle, une densité de rayonnement non nulle à notre époque, équivalente à un rayonnement de corps noir dont la température actuelle devrait être de l'ordre de grandeur $1-10 K$. Cependant, à l'époque, l'idée de Big Bang demeure assez spéculative et souffre de plusieurs problèmes^[?] et la nucléosynthèse primordiale semble être une impasse puisqu'elle échoue apparemment à donner une explication exhaustive de la courbe d'abondance des éléments. Pour ces raisons, ces résultats n'attirent pas vraiment l'attention au moment de leur publication.

Les équations de Friedmann sont les équations qui décrivent un Univers homogène isotrope obéissant aux équations d'Einstein. Pour un univers de facteur d'échelle $a$, de rayon de courbure $R$ et constitué de différentes formes d'énergie de densités $\rho_i$, de pression $P_i$ et d'équation d'état $f_i(\rho_i,P_i) = 0$ :\begin{equation}\left\{\begin{matrix} \dot{a}^2-\dfrac{8 \pi G}{3c^2} \displaystyle \sum_i \rho_i a^2 & = & \dfrac{kc^2}{R^2} & \mbox{ (1)}\\ \dfrac{d}{dt}\left ( \rho_i a^3 \right ) & = & -P_i \dfrac{d}{dt} \left (a^3 \right) & \mbox{ (2)}\\ f_i(\rho_i,P_i) & = &0 & \mbox{ (3)}\\ \end{matrix}\right.\end{equation} La première équation décrit la dynamique de l'Univers en fonction de son contenu. La seconde équation traduit le premier principe de la thermodynamique. La troisième équation indique simplement la relation entre densité et pression imposée par l'équation d'état de la $i$-ème forme d'énergie. On distingue trois formes d'énergie caractéristiques d'équations d'état particulières :

• La matière "froide" (aussi dite non relativiste ou poussière). C'est la matière ordinaire massive dont la vitesse est très inférieure à celle de la lumière. Pour un gaz parfait non relativiste, $P/\rho \propto v^2/c^2$ et on peut considérer $P = 0$. L'équation (2) donne alors $\rho a^3 = \mbox{ cste } = \rho_0$.
• Les rayonnements. C'est la lumière ou de la matière ultrarelativiste comme les neutrinos ($v\sim c$). L'équation d'état est alors $P = \rho/3$. L'équation (2) donne cette fois $\rho a^4 = \mbox{ cste } = \rho_0$.
• L'énergie du vide. Cette énergie d'équation d'état $P=-\rho$ est équivalente à l'introduction d'une constante cosmologique. Selon l'équation (2), $\rho = \mbox{cste} = \rho_0$.
• De façon plus générale, pour une énergie d'équation d'état $P=w\rho$ où $w$ est une constante, alors l'équation (2) implique $\rho a^{3(1+w)} = \mbox{cste}$

Paramètres de densité

On divise l'équation (1) par le carré de la constante de Hubble actuelle $H_0 = \dot{a}/a (t=0)$, puis on la redivise par $a^2$. On trouve alors : \begin{equation} \dfrac{1}{H_0^2} \left (\dfrac{\dot{a}}{a}\right )^2 - \displaystyle \sum_i \dfrac{\rho_i(t)}{\rho_c} = \dfrac{kc^2}{R^2 H_0^2 a^2} \end{equation} Où l'on a introduit la densité critique $\rho_c$ : \begin{equation} \rho_c = \dfrac{3c^2 H_0^2}{8\pi G} \end{equation} On suppose que l'Univers est constitué de matière froide ($\rho_m = \rho_m^0/a^3$), de rayonnement ($\rho_r = \rho_r^0/a^4$), d'énergie du vide ($\rho_v = \rho_v^0$) et d'une espèce telle que $P = w\rho$ donc $\rho_w = \rho_w^0 a^{-3(1+w)}$. On définit le rapport entre la densité d'une espèce aujourd'hui et la densité critique actuelle comme : \begin{equation} \Omega_i \equiv \dfrac{\rho_i^0}{\rho_c} \end{equation} On définit par ailleurs le paramètre de courbure $\Omega_k$ tel que : \begin{equation} \Omega_k = \dfrac{kc^2}{R^2 H_0^2} \end{equation} Alors la dynamique du facteur d'échelle est donnée par : \begin{equation} \dfrac{1}{H_0^2} \left (\dfrac{\dot{a}}{a}\right )^2 - \left ( \dfrac{\Omega_m}{a^3} + \dfrac{\Omega_r}{a^4} + \Omega_v + \dfrac{\Omega_w}{a^{3(1+w)}}\right ) = \dfrac{\Omega_k}{a^2} \end{equation} Les quantités $\Omega_i$ sont appelées "paramètres de densité", et sont plus souvent utilisées que les densités elles mêmes. Leur valeur indique la proportion d'énergie contenue sous une forme précise. En évaluant l'équation à $t=0$ il vient : \begin{equation} 1-\Omega_m - \Omega_r - \Omega_v - \Omega_w = \Omega_k \end{equation} Cette équation signifie que la courbure de l'Univers est imposée différence entre la densité critique et la densité totale $\rho_{total}$. Une densité totale inférieure à $\rho_c$ implique $\Omega_k > 0$ et donc un Univers hyperbolique. A l'inverse, $\rho_{total} < \rho_c$ implique une géométrie sphérique. Le cas d'égalité correspond à un Univers plat.

Démonstration

Solutions particulières de l'équation de Friedmann

On peut résoudre l'équation de Friedmann dans un certain nombre de configurations particulières. Par exemple on peut considérer en effet que l'Univers est dominé par une certaine forme d'énergie

Univers de poussière

Dans un tel univers, $P=0$. De là le facteur d'échelle obéit à l'équation : \begin{equation} \dot{a}^2 - H_0^2\dfrac{\Omega_m}{a} = \dfrac{kc^2}{R^2} = H_0^2 \Omega_k = H_0^2 (1-\Omega_m) \end{equation} Cette équation ressemble beaucoup à l'équation du mouvement d'une particule-test dans le champ gravitationnel d'une masse $M$ (problème à deux corps) : \begin{equation} \dfrac{1}{2}\dot{x}^2 - \dfrac{GM}{x} = E \end{equation} Cela est naturel puisque la matière froide n'est pas relativiste et la matière non relativiste est décrite par la mécanique newtonienne. Il y a alors 3 solutions possibles selon le signe de $k/R^2$, de même qu'il existe trois solutions possibles au problème à deux corps (trajectoire hyperbolique, parabolique ou elliptique).

• Pour un Univers plat ($k/R^2 = 0$, $\Omega_m = 1$), en expansion, la solution est alors, si $a(0) = 1$ où $t=0$ désigne l'époque actuelle : \begin{equation} a^{3/2}(t) = 1 + \dfrac{3}{2} H_0 t \end{equation} Cet univers "nait" à $t= - \dfrac{2}{3} H_0$ et ne cesse de s'expandre depuis. Son âge est donc $T = \dfrac{2}{3} H_0$.
• Pour un Univers sphérique ($k/R^2 < 0$, $\Omega_m > 1$), la solution est alors : \begin{equation} \left ( \dfrac{\Omega_m}{\Omega_m-1}\right)^{3/2} \left [ u\sqrt{1-u^2}-\sin^{-1} u\right ]_{ \sqrt{(\Omega_m-1)/\Omega_m}}^{ \sqrt{a(\Omega_m-1)/\Omega_m}} = \mp \sqrt{\Omega_m} t \end{equation}
• Pour un Univers hyperbolique ($\Omega_m < 1$) : \begin{equation} \left ( \dfrac{\Omega_m}{(1-\Omega_m)}\right)^{3/2} \left [ u\sqrt{1+u^2}-\sinh^{-1} u\right ]_{ \sqrt{(1-\Omega_m)/\Omega_m}}^{ \sqrt{a(1-\Omega_m)/\Omega_m}} = \pm \sqrt{\Omega_m} t \end{equation}

Facteur d'échelle d'un univers dominé par de la matière non relativiste (gnuplot)

Évolution du facteur d'échelle pour un Univers dominé par la poussière et pour différentes valeurs de $\Omega_m$.

Univers de rayonnement (ou de lumière)

Un univers dominé par les radiations obéit à l'équation d'état $P = \rho/3$. L'équation (2) donne alors $\rho a^4 = \mbox{ cste } = \rho_0$. Alors l'équation à résoudre est : \begin{equation} \dot{a}^2 - H_0^2 \dfrac{\Omega_r}{a^2} = H_0^2(1-\Omega_r) \end{equation} On suppose par ailleurs $\dot{a} > 0$.

• La solution en Univers plat est alors simple : $a^2(t) - 1 = 2 H_0 t$
• Pour $k \neq 0$ ($\Omega_r \neq 1$) \begin{equation} \dfrac{1}{1-\Omega_r} \left [ \sqrt{(1-\Omega_r) a^2+ \Omega_r} - 1 \right ] = H_0 t \end{equation} Si de plus $k<0$ (géométrie sphérique), alors l'Univers atteint une densité minimale ($a \leq \sqrt{\dfrac{\Omega_r}{\Omega_r-1}}$) puis se recontracte. Preuve :
  Afficher/Masquer

  On réécrit l'équation sous la forme : \begin{equation} \left (\dfrac{da}{dt} \right )^2 - \dfrac{\beta}{a^2} = \alpha \end{equation} Qu'on résout par séparation des variables : \begin{equation} \dfrac{da}{\sqrt{\alpha + \beta/a^2}} = \dfrac{a da}{\sqrt{\alpha a^2 + \beta}} = dt \end{equation} Ce qui intégré entre $a(t=0)=1$ et $a(t)$ donne : \begin{equation} \dfrac{1}{\alpha} \left ( \sqrt{\alpha a^2 + \beta} - \sqrt{\alpha+\beta} \right ) = t \end{equation} Cet Univers existe tant que $a^2 \geq - \dfrac{\alpha}{\beta}$. Si $k<0$, alors ceci requiert $a \geq \sqrt{\dfrac{-\alpha}{\beta}} = a_{min}$. Ce facteur d'échelle minimum est atteint pour $t = -\sqrt{\alpha+\beta}$.

Facteur d'échelle d'un univers dominé par le rayonnement (gnuplot)
Évolution du facteur d'échelle pour un Univers dominé par le rayonnement pour différentes valeurs de $\Omega_r$.

Univers d'énergie du vide

L'énergie du vide a pour équation d'état $P=-\rho$ ce qui après résolution de (2) donne $\rho = \mbox{ cste } = \rho_0$. Dès lors : \begin{equation} \dot{a}^2 - H_0^2 \Omega_{\Lambda} a^2 = H_0^2 (1-\Omega_{\Lambda}) \end{equation}

• La solution en Univers plat est alors : \begin{equation} a(t) = \exp{\left( H_0 t\right )} \end{equation} Un tel Univers peut alors s'expandre ou se contracter de façon exponentielle.
• $k>0$, $\Omega_{\Lambda} < 1$ (géométrie hyperbolique) \begin{equation}\left\{\begin{matrix} a(t) = &A\sinh \left [ H_0 \sqrt{\Omega_{\Lambda}}(t+T) \right ] \\ T = &\pm \tau \tanh^{-1} \sqrt{\Omega_{\Lambda}} \\ A = &\sqrt{\dfrac{1-\Omega_{\Lambda}}{\Omega_{\Lambda}}} \\ \tau = & 1/H_0 \sqrt{\Omega_{\Lambda}} \\ \end{matrix}\right.\end{equation} Cet Univers atteint une densité infinie à la date $T$, soit antérieure, soit postérieure à la date actuelle.
• $k<0$, $\Omega_{\Lambda} > 1$(géométrie sphérique) : \begin{equation}\left\{\begin{matrix} a(t) = &A\cosh \left [ H_0 \sqrt{\Omega_{\Lambda}} (t+T) \right ] \\ T = &\pm \tau \tanh^{-1} 1/\sqrt{\Omega_{\Lambda}} \\ A = &\sqrt{\dfrac{\Omega_{\Lambda}-1}{\Omega_{\Lambda}}} \\ \tau = & 1/H_0 \sqrt{\Omega_{\Lambda}} \\ \end{matrix}\right.\end{equation} Cet Univers atteint une densité maximale à la date $T$, soit antérieure, soit postérieure à la date actuelle.
Preuve
Afficher/Masquer
L'équation de Friedmann peut être réécrite sous la forme \begin{equation} \dot{a}^2 - \beta a^2 = \alpha \end{equation} En la dérivant il vient alors : \begin{equation} \ddot{a} - \beta a = 0 \end{equation} La solution générale de cette équation a donc pour forme : \begin{equation} a(t) = \lambda \cosh(\sqrt{\beta} t) + \mu \sinh(\sqrt{\beta} t) \end{equation} Par ailleurs $a(0) = 1$ donc $\lambda = 1$. D'autre part $\dot{a}^2(0) = \alpha+\beta$ Donc $\mu ^2 \beta = \alpha + \beta$ et $\mu = \pm \sqrt{1+\dfrac{\alpha}{\beta}}$ Et finalement : \begin{equation} a(t) = \cosh(\sqrt{\beta} t) \pm \sqrt{1+\dfrac{\alpha}{\beta}} \sinh(\sqrt{\beta} t) \end{equation} On veut mettre ceci sous la forme $a(t) = A \cosh {\sqrt{\beta}(t-T)}$. On utilise pour cela la relation $\cosh (x+y) = \cosh(x) \cosh(y) + \sinh(x) \sinh(y)$. On a alors : \begin{equation} A \cosh {\sqrt{\beta}t} \cosh {\sqrt{\beta}T} - A \sinh {\sqrt{\beta}t} \sinh {\sqrt{\beta}T} \\ = \cosh(\sqrt{\beta} t) \pm \sqrt{1+\dfrac{\alpha}{\beta}} \sinh(\sqrt{\beta} t) \end{equation} De cela on tire à la fois $A\cosh {\sqrt{\beta}T} = 1$ et $\pm A\sinh{\sqrt{\beta}T} = \sqrt{1+\dfrac{\alpha}{\beta}}$. Ce qui entraine : \begin{equation}\left\{\begin{matrix} T = & \mp \dfrac{1}{\sqrt{\beta}} \tanh^{-1} \sqrt{1+\dfrac{\alpha}{\beta}} \\ A = & \sqrt{-\dfrac{\alpha}{\beta}} \end{matrix}\right.\end{equation} Ceci n'est donc possible que si $\alpha < 0$. Dans ce cas on a bien : \begin{equation} a(t) = -\sqrt{\dfrac{\alpha}{\beta}} \cosh { \left [ \sqrt{\beta} t - \tanh^{-1} \sqrt{1+\dfrac{\alpha}{\beta}}\right ] } \end{equation} Dans le cas $\alpha > 0$, on peut écrire $a(t)$ sous la forme $A \sinh {\sqrt{\beta}(t-T)}$. On invoque cette fois l'égalité $\sinh (x+y) = \sinh(x)\cosh(y) + \sinh(y)\cosh(x)$. Cette fois il apparait que : \begin{equation}\left\{\begin{matrix} T = & \mp \dfrac{1}{\sqrt{\beta}} \tanh^{-1} \sqrt{\dfrac{1}{1+\dfrac{\alpha}{\beta}}} \\ A = & \sqrt{+\dfrac{\alpha}{\beta}} \end{matrix}\right.\end{equation} Enfin, si $\alpha = 0$, alors $\mu = \pm 1$, donc $a(t) = \exp{\dfrac{1}{\sqrt{\beta}}t}$
Notons que si l'énergie du vide est l'effet d'une constante cosmologique $\Lambda$ non nulle alors $\Omega_{\Lambda} = \Lambda c^2/3H_0^2$.

Facteur d'échelle d'un univers dominé par la constante cosmologique (gnuplot)
Évolution du facteur d'échelle pour un Univers dominé par la constante cosmologique (ou l'énergie du vide si $w=-1$) pour différentes valeurs de $\Omega_\Lambda$.

Univers vide

Un univers vide vérifie simplement l'équation \begin{equation} \dot{a}^2 = H_0^2 \Omega_{k} = H_0^2 \end{equation} Un tel Univers ne peut être de géométrie sphérique ! Il est hyperbolique ou plat en l'absence d'expansion. La solution est alors : \begin{equation} a(t) = \pm H_0 t + 1 \end{equation} L'âge d'un tel Univers (s'il est en expansion) ou son espérance de vie (s'il est en contraction) est alors $T = R/c = 1/H_0$. Un Univers plat et vide est statique.