La rédaction de contenu n'est pas achevée. Les informations peuvent être incomplètes ou contenir des erreurs.
Une supernova de type Ia (thermonucléaire) est le phénomène très lumineux d'explosion d'une naine blanche lorsque celle-ci
en accrétant de la matière devient trop massive pour demeurer stable. Les supernovae Ia sont très intéressantes en cosmologie,
car ce sont des chandelles standard, similairement aux céphéides. Elles permettent donc d'effectuer des mesures de distance de luminosité. Étant très lumineuses, elles sont détectables même étant lointaines, jusqu'à des redshift dépassant 1. Or, à ces redshift,
la dépendance de la distance de luminosité avec le redshift dépend beaucoup du modèle cosmologique, et donc les supernovae permettent de mesurer assez précisément des
paramètres cosmologiques. C'est par leur étude que fut découverte l'accélération de l'expansion de l'Univers.
Cette annexe est divisée en trois parties :
- Naines blanches et masse de Chandrasekhar
- Effondremment
- Emploi comme chandelles standards
Les naines blanches, masse de Chandrasekhar
Les naines blanches sont des étoiles très compactes ($m\sim M_{\odot}$ et $R \sim 1\% \cdot R_{\odot}$), principalement constituées
de carbone et d'oxygène, qui ne résistent à l'effondrement gravitationnel non pas par des réactions thermonucléaires en leur
sein puisque celles-ci ne sont plus prédominantes, mais grâce à la pression de dégénérescence de leurs électrons, d'origine
quantique. La suite de ce paragraphe consiste à montrer l'existence d'une masse limite pour ces objets, appelée masse de Chandrasekhar,
au-delà de laquelle cette pression de dégénérescence est insuffisante pour soutenir le poids de la naine blanche.
Equation d'état du gaz d'électrons
On considère l'ensemble des électrons qui constituent l'étoile. Ceux-ci sont confinés à d'importantes pressions et densités,
et leur comportement est à la fois quantique et relativiste.
On cherche à établir l'équation d'état du gaz d'électrons.
Pour les décrire, on apparente le système qu'ils forment à une boite de dimension $L\times L \times L$ remplie d'électrons.
Pour commencer, il faut déterminer les différents états microscopiques autorisés. Pour cela on résout l'équation de Dirac
(pour conserver une description quantique et relativiste), en considérant que les électrons ne peuvent s'échapper de la boite
(fonction d'onde nulle aux bords) :
\begin{equation}
i\hbar \gamma^\mu \partial_\mu \psi - mc \psi = 0 \mbox{ et } \psi (t, \vec{x}) = 0 \mbox{ si } x_i \in \{ 0, L \}
\end{equation}
En recherchant les solutions sous formes d'ondes on trouve :
\begin{equation}
\psi (t,\vec{x}) = \begin{pmatrix}
\phi\\
\left [ \dfrac{\vec{\sigma} \vec{p}}{E+mc^2} \right ] \phi
\end{pmatrix} e^{\frac{i}{\hbar}\left( Et - \vec{p} \cdot \vec{x}\right )}
\end{equation}
où $E = +\sqrt{m^2c^4 + p^2c^2}$, l'expression relativiste de l'énergie.
L'application des conditions aux limites donne $p_i = h n_i / L$ avec $n_i \in \mathbb{Z}$. (Même résultat avec l'équation
de Schrodinger, donc non relativiste).
Maintenant que l'on connait l'ensemble des micro-états, la question est de connaitre les grandeurs thermodynamiques que sont
la densité, la densité d'énergie et la pression et de les relier.
On définit la fonction $f_i(E_i)$ définie comme le nombre d'électrons dans l'état $i$.
Les électrons étant des fermions, pour un équilibre thermique, ils suivent la distribution de Fermi-Dirac. Ainsi, le nombre
d'électrons $n_i$ dans un état $i$ est dans ce cas donné par :
\begin{equation}
f_i(E_i) = \dfrac{g}{e^{E_i/k_B T} + 1}
\end{equation}
Où $g$ est la dégénérescence de spin (pour un spin 1/2 comme c'est le cas pour les électrons, $g=2$).
Ici, chaque état est déterminé par les nombres quantique $n_x,n_y,n_z$ tels que $p^2 = \frac{h^2}{L^2} (n_x^2 + n_y^2 + n_z^2)$.
Le nombre $N$ d'électrons est donné par la somme des espérances moyennes associées à chaque état :
\begin{equation}
N = f_i(E_i) = g \sum_{n_x = -\infty}^{+\infty} \displaystyle \sum_{n_y = -\infty}^{+\infty} \displaystyle \sum_{n_z = -\infty}^{+\infty}
f \left (E(n_x, n_y, n_z)\right )
\end{equation}
Remarquons que les niveaux d'impulsions (et donc d'énergie) sont de moins en moins espacés quand $L\to +\infty$, si bien que
l'écart entre deux niveaux consécutifs devient infinitésimal.
On peut donc transformer les sommes en intégrales selon :[?]
\begin{equation}
\sum_{n_x = -\infty}^{+\infty} \to \dfrac{L}{h} \displaystyle\int_{-\infty}^{+\infty} dp_x
\end{equation}
L'expression du nombre d'électrons $N$ devient alors :
\begin{equation}
N = g\dfrac{L^3}{h^3} \displaystyle\int_{-\infty}^{+\infty} \displaystyle\int_{-\infty}^{+\infty} \displaystyle\int_{-\infty}^{+\infty}
f \left (E(p_x, p_y, p_z)\right ) dp_x dp_y dp_z
\end{equation}
L'intégrande ne dépendant que de $E$ qui ne dépend que de la norme de $\vec{p}$ (pas de sa direction), il est intéressant
de passer en coordonnées sphériques :
\begin{equation}
N = g\dfrac{L^3}{h^3} \displaystyle\int_{\theta = 0}^{2\pi} \displaystyle\int_{\phi = 0}^{\pi} \displaystyle\int_{p = 0}^{+\infty}p^2
\sin{(\phi)} f(E(p))dp \\ = 4\pi g\dfrac{L^3}{h^3} \displaystyle\int_{0}^{+\infty} f(E(p)) p^2 dp
\end{equation}
Enfin, la densité d'électrons $n$ vaut simplement $N/L^3$ et donc :
\begin{equation}
n =\dfrac{ 4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} f(E(p)) p^2 dp
\end{equation}
L'énergie totale du système $U$ est donnée par la somme des énergies moyennes de chaque état $U_i = f_i E_i$. En sommant sur
tous les états autorisés on trouve :
\begin{equation}
U = g \displaystyle \sum_{n_x = -\infty}^{+\infty} \displaystyle \sum_{n_y = -\infty}^{+\infty} \displaystyle \sum_{n_z =
-\infty}^{+\infty} f \left (E(p_x, p_y, p_z)\right ) E(n_x, n_y, n_z)
\end{equation}
Cette somme peut être transformée en intégrale par le même processus de continuisation que précédemment. La seule différence
est la présence d'un facteur $E$ supplémentaire dans l'intégrale :
\begin{equation}
U = 4\pi g\dfrac{L^3}{h^3} \displaystyle\int_{0}^{+\infty} f \left (E(p)\right ) E(p) p^2 dp
\end{equation}
La densité d'énergie est simplement $\rho = U/L^3$, et donc :
\begin{equation}
\rho = \dfrac{4\pi g}{h^3} \displaystyle\int_{0}^{+\infty}f \left (E(p)\right ) E(p) p^2 dp
\end{equation}
La pression des électrons d'impulsion $p$ est $pv/3$ [?]
Par ailleurs $v = pc^2/E$.
[?] De là :
\begin{equation}
P = \dfrac{4\pi g}{3h^3} \displaystyle\int_{0}^{+\infty}f \left (E(p)\right ) \dfrac{p^4 c^2}{E(p)} dp
\end{equation}
Si les électrons sont à l'équilibre thermique, ils suivent la distribution de fermi-dirac et donc :
\begin{equation}\left\{\begin{matrix}
n & = & \dfrac{ 4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} \dfrac{p^2 dp}{e^{E(p)/k_B T} + 1}\\
\rho & = & \dfrac{4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} \dfrac{p^2 E(p) dp}{e^{E(p)/k_B T} + 1} \\
P & = & \dfrac{4\pi g}{3h^3} \displaystyle\int_{0}^{+\infty} \dfrac{1}{E(p)} \dfrac{p^4 c^2 dp}{e^{E(p)/k_B T} + 1}
\end{matrix}\right.\end{equation}
Les intégrales peuvent être réécrites à l'aide des variables $u = E/mc^2 = 1+\frac{p^2}{m^2c^2}$ et $x = mc^2/(k_B T)$ :
\begin{equation}\left\{\begin{matrix}
n & = & \dfrac{ 4\pi g m^3 c^3}{h^3} \displaystyle\int_{1}^{+\infty} \dfrac{u \sqrt{u^2-1} du}{e^{ux} + 1}\\
\rho & = & \dfrac{4\pi g m^4 c^5}{h^3} \displaystyle\int_{1}^{+\infty} \dfrac{u^2 \sqrt{u^2-1} du}{e^{ux} + 1} \\
P & = & \dfrac{4\pi g m^4 c^5}{3h^3} \displaystyle\int_{1}^{+\infty} \dfrac{(u^2-1)^{3/2} du}{e^{ux} + 1}
\end{matrix}\right.\end{equation}
On s'intéresse ici à l'équation d'état $n \to P (n)$ puisque la relation nécessaire à la résolution du problème est celle
entre la densité de masse d'électrons $\rho_m = n m$ et la pression $P$.
Les intégrales peuvent être évaluées numériquement.
Si les effets thermiques ne dominent plus, un cas extrême à envisager est le cas où tous les niveaux en dessous d'une certaine
énergie de seuil $E_F$ sont occupé. On parle d'état dégénéré. Ceci permet de maximiser la densité d'électrons à une énergie
totale donnée. Dans ce cas la fonction $f(E)$ vaut 1 en dessous de $E_F$ et 0 au dessus :
\begin{equation}
f_d(E) = \left\{\begin{matrix}
1 & \mbox{ si } & E \leq E_F \\
0 & \mbox{ si } & E > E_F
\end{matrix}\right.
\end{equation}
Et donc :
\begin{equation}\left\{\begin{matrix}
n_d & = & \dfrac{ 4\pi g m^3 c^3}{h^3} \displaystyle\int_{1}^{u_F} u \sqrt{u^2-1} du\\
P_d & = & \dfrac{4\pi g m^4 c^5}{3h^3} \displaystyle\int_{1}^{u_F} (u^2-1)^{3/2} du
\end{matrix}\right.\end{equation}
On note $n_0 = \dfrac{ 4\pi g m^3 c^3}{h^3} $ et $P_0 = \dfrac{4\pi g m^4 c^5}{3h^3}$.
Le régime dégénéré peut être résolu analytiquement :
\begin{equation}
\displaystyle\int_{1}^{u_F} u \sqrt{u^2-1} du = \dfrac{1}{2} \displaystyle\int_{0}^{u_F^2 - 1} \sqrt{t} dt = \dfrac{1}{3}
\left (u_F^2 - 1\right )^{3/2}
\end{equation}
Et
\begin{equation}
\displaystyle\int_{1}^{u_F} (u^2-1)^{3/2} du = \displaystyle\int_{0}^{\cosh^{-1} u_F}\sinh^4{(t)} dt \\
= \dfrac{3}{8} \cosh^{-1} u_F - \dfrac{1}{2} u_F \sqrt{u_F^2 - 1} + \dfrac{1}{8} u_F \sqrt{u_F^2 - 1} (2u_F^2 - 1)
\end{equation}
Ce qui donne, en définissant $x \equiv 3\dfrac{n}{n_0}$ :
\begin{equation}
P = P_0 \left [ \dfrac{3}{8} \sinh^{-1}{\left (x^{1/3} \right )} + \sqrt{1+ x^{2/3}} \left ( \dfrac{1}{4}x- \dfrac{3}{8}
x^{1/3} \right ) \right ]
\end{equation}
Similairement on peut montrer que la densité d'énergie peut s'écrire :
\begin{equation}
\rho_e =\dfrac{3}{8} P_0 \left [ \sinh^{-1}{\left (x^{1/3} \right )} + \sqrt{1+ x^{2/3}} \left ( 2x- x^{1/3} \right ) \right
]
\end{equation}
Les courbes $n/n_0 \mapsto P/P_0$ sont calculées numériquement (facteurs dimensionnés exclus). On trouve
On observe pour un gaz dégénéré deux régimes différents :
- Faible densité : $P \sim P_0 \left ( \dfrac{n}{n_0} \right )^{5/3}$ (courbe en pointillés)
- Haute densité : $P \sim P_0 \left ( \dfrac{n}{n_0} \right )^{4/3}$ (courbe en traits discontinus)
Un gaz dicté par les effets thermiques se comporte comme un gaz dégénéré à forte densité et comme un gaz parfait à basse densité.
(La relation pression/densité pour fermi dirac est une droite,
Résistance à la gravité
Dans une naine blanche, la force qui compense la pression de dégénérescence des électrons est la gravité. On peut montrer
à partir de la relativité générale que l'équilibre se traduit par l'équation de Tolman-Oppenheimer :
\begin{equation}
\left( 1 - \frac{2 G M(r)}{c^2 r} \right) P'(r) = - \frac{G}{r^2}\dfrac{1}{c^2} \left( \rho_m(r) + \rho_e(r) + P(r) \right)
\left(M(r) + 4 \pi r^3 \frac{P(r)}{c^2} \right)
\end{equation}
$P$ est la pression, $\rho_m$ la densité d'énergie de masse de la matière baryonique (qui constitue l'essentiel de la masse
d'une étoile), et $\rho_e$ celle du gaz d'électrons. $M(r)$ est la masse comprise dans la sphère de rayon $r$ centrée au coeur
de l'étoile.
La pression qui domine est celle de dégénérescence donc $P$ est la pression du gaz d'électrons.
Par ailleurs la masse est reliée à la densité de matière et d'énergie par :
et \begin{equation}
M'(r) = 4\pi r^2 \dfrac{\rho_m(r) + \rho_e(r)}{c^2}
\end{equation}
On peut écrire $\rho_m \simeq n_b m_p c^2 $. où on définit le rapport entre densité baryonique et d'électron $\mu \equiv n_b
/ n_e$. Alors on a $n_e = \rho_m / (\mu m_p c^2)$. En définissant $\rho_0 \equiv n_0 m_p c^2$, il vient que $x = 3 \rho_m
/ (\mu \rho_0)$.
Les naines blanches étant principalement constituées d'éléments tels que le carbone, il y a en moyenne un proton et un neutron
pour chaque électron donc $\mu = 2$
On définit les variables adimensionnées associées :
$p \equiv P/P_0$, $\epsilon = \rho_e/\rho_0$, $\xi = r/R_{\odot}$ et $m = M/M_{\odot}$
L'équation devient :
\begin{equation}
\left( 1 - \frac{2 G M_{\odot} m(\xi)}{c^2 R_{\odot} \xi} \right) \dfrac{P_0R_{\odot}^2 }{G R_{\odot}}p'(\xi) = - \frac{1}{\xi^2
c^2} \left( \rho_0 \mu x/ 3 + \rho_0 \epsilon + P_0 p(\xi) \right) \left(M_{\odot} m(\xi) + 4 \pi R_{\odot}^3 \xi^3 \frac{P_0
p(\xi)}{c^2} \right)
\end{equation}
En définissant les variables adimensionnées $\alpha \equiv \dfrac{P_0}{\rho_0} = \dfrac{m_e}{3 m_p}$ et $\beta = \dfrac{\rho_0
R_{\odot}^3}{M_{\odot}c^2} = \dfrac{ 4\pi g m_e^3 m_H c^3}{h^3} \dfrac{R_{\odot}^3}{M_{\odot}}$ ainsi que le rayon de schwarszchild
du Soleil $r_s = 2GM_{\odot}/c^2$ alors :
[?]
\begin{equation}
2 \alpha \dfrac{R_{\odot}}{r_s} \left( 1 - \frac{r_s m(\xi)}{R_{\odot} \xi} \right) p'(\xi) = - \frac{1}{\xi^2} \left( \mu
x (\xi) /3 + \epsilon(\xi) + \alpha p(\xi) \right) \left( m(\xi) + 4 \alpha \beta \pi \xi^3 p(\xi) \right)
\end{equation}
Et par ailleurs :
\begin{equation}
m'(\xi) = 4\pi \xi^2 \dfrac{\rho(\xi)}{\rho_0} = \dfrac{4}{3} \pi\xi^2 \dfrac{\rho_0 R_{\odot}^3}{M_{\odot}}(\mu x + 3\epsilon
)
\end{equation}
On peut aussi employer l'équation hydrostatique non relativiste :
\begin{equation}
2 \alpha \dfrac{R_{\odot}}{r_s}p'(\xi) = -\dfrac{\mu m(\xi) x(\xi)}{3 \xi^2}
\end{equation}
Résultat
Les équations d'équilibre sont résolues (Relativité générale ou gravitation newtonienne) et conduisent au résultat suivant
:
Effondrement et supernova
On estime que le mécanisme d'effondrement d'une naine blanche donnant lieu a une supernova de type Ia est le suivant :
(F. Hoyle, William A. Fowler
1960)
- La naine blanche accrète de la matière en général d'une étoile compagnon telle qu'une géante rouge. Sa masse augmente jusqu'à
devenir suffisamment proche de la limite de Chandrasekhar. Celle-ci devient alors instable (la pression de dégénerescence
ne permet plus de contrer la gravité).
Emploi comme chandelles standards
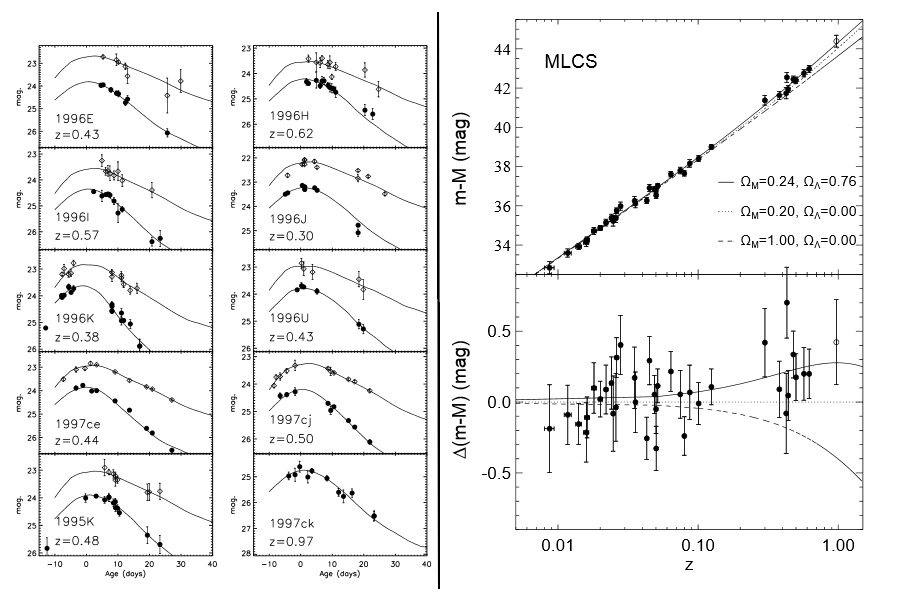
De façon empirique, on sait au début des années 1990 que les supernovae de type Ia ont une magnitude maximale similaire, et des courbes de luminosité ($t\mapsto L(t)$) semblables.
Ces courbes montrent toute une augmentation rapide jusqu'à l'atteinte d'une maximum puis une diminution plus lente.
De là, elles possèdent un certain potentiel en tant que chandelles standard. Une bonne chandelle standard doit avoir une dispersion
en magnitude $\Delta M$ faible, pour que la méthode soit précise. Les
céphéides variables par exemple, peuvent avoir des
magnitudes absolues très différentes, mais celle-ci est fortement corrélée avec leur période - qui est facilement mesurable - si bien
qu'on peut déduire leur
magnitude intrinsèque avec une dispersion $\Delta M_{V} \sim $ 0,1
(L. N. Berdnikov, A. K. Dambis
et al.
1997)
.
En 1993, Phillips montre à partir de mesures effectuées sur 9 SNe Ia proches
(M. M. Phillips
1993)
que celles-ci possèdent une dispersion en magnitude maximale intrinsèque de l'ordre de $\pm 0,6$ dans la bande V, et $\pm
0,8$ dans la bande B. Il cite notamment le cas de la supernova SN 1991bg qui est significativement moins lumineuses que les
autres. Il note aussi que sa courbe de luminosité dans la bande B au cours du temps semble décroître plus rapidement. Des
corrélations sont alors recherchées afin de déterminer si l'estimation de la luminosité maximale peut être affinée à l'aide
d'autres observables. Dans la poursuite de l'idée des travaux de Pskovskii en 1984, Phillips teste l'hypothèse d'une corrélation
entre rapidité du déclin de la luminosité des
supernovae Ia et leur luminosité maximale. Il définit dans ce but un paramètre de déclin noté $\Delta m_{15}(B)$ qui correspond à la variation
de
magnitude apparente entre le pic de luminosité et 15 jours plus tard.
Par la suite cette méthode est encore améliorée, à l'aide de templates ou de remises à l'échelle appliquées aux courbes de
lumière
(G. Goldhaber, D. E. Groom
et al.
2001)
.
(Adam G. Riess, Alexei V. Filippenko
et al.
1998)
(S. Perlmutter, G. Aldering
et al.
1999)
Ceci ne dépend pas de $L$ puisque la limite $L\to \infty$ que nous avons considérée supprime les effets de bords. Cette équation
est vraie pour des systèmes de taille $L \gg L_0 = \dfrac{hc}{k_B T}$. A T = 1000 K (donc vraiment en dessous du minimum pour
une étoile), $L_0 \sim 1 \mbox{ m}$, ce qui est négligeable par rapport à la taille de l'étoile. Cette relation est donc valable
à l'échelle locale : on peut l'appliquer au contenu de l'étoile entre $r$ et $r+dr$.
La pression est la quantité de mouvement transmise à une paroi contenant le gaz par unité de surface et de temps. Montrer
pv/3
\begin{equation}p = \dfrac{mv}{\sqrt{1-v^2/c^2}}\end{equation}
donc \begin{equation}v^2\left (1+\frac{p^2}{m^2c^2} \right ) = \frac{p^2}{m^2c^2}\end{equation}
et \begin{equation}v^2 = \dfrac{p^2}{m^2 + p^2/c^2} = \dfrac{p^2 c^4}{E^2}\end{equation}
\begin{equation}
\left( 1 - \frac{2 G M_{\odot} m(\xi)}{c^2 R_{\odot} \xi} \right) \dfrac{P_0R_{\odot }}{G M_{\odot}\rho_0}p'(\xi) =
-\frac{1}{\xi^2 } \left( \mu x (\xi)/ 3+ \epsilon + \dfrac{P_0}{\rho_0} p(\xi) \right) \left(M_{\odot} m(\xi) + 4 \pi R_{\odot}^3
\xi^3 \frac{P_0 p(\xi)}{c^2} \right)
\end{equation}
\begin{equation}
\left( 1 - \frac{r_s m(\xi)}{R_{\odot} \xi} \right) 2 \alpha \dfrac{R_{\odot}}{r_s} p'(\xi) = -\frac{1}{\xi^2} \left(
\mu x (\xi)/ 3 + \epsilon(\xi) + \alpha p(\xi) \right) \left(M_{\odot} m(\xi) + 4 \pi R_{\odot}^3 \xi^3 \frac{P_0 p(\xi)}{c^2}
\right)
\end{equation}