La rédaction de contenu n'est pas achevée. Les informations peuvent être incomplètes ou contenir des erreurs.
Au début des années 1990, le modèle le plus accepté parmi les cosmologistes est le modèle $S-CDM$, c'est-à-dire un Univers
proche de sa densité de fermeture (plat) constitué en quasi totalité de matière noire froide, et également de matière baryonique
froide. Ce modèle montre de plus en plus de faiblesses d'après les dernières observations, et de nouvelles données observationnelles
sont nécessaires pour en comprendre les raisons.
Les supernovae sont des évènements consécutifs à la "mort" d'une étoile. Ils libèrent une énergie colossale et sont donc très
lumineux. Au début des années 1990, on distingue deux catégories principales de supernovae (SN) :
- Les supernovae thermonucléaires (aussi appelées supernovae de type Ia) : Elles sont dues à l'effondrement de naines blanches (des étoiles compactes de masse proche de celle du Soleil mais de
rayon 100 fois plus petit) maintenues en équilibre contre l'effondrement gravitationnel par la pression de dégénérescence
de leurs électrons[?]
- Les supernovae à effondrement de coeur : Elles sont dues à l'effondrement d'une plus grande variétés d'étoiles massives (masse supérieure à une dizaine de masses
solaires) dès lors que leur coeur produit du Fer.
Les
supernovae de type Ia se différencient des autres supernovae de type I par la présence de silicium dans leur spectre. Elles sont surtout comme
propriété majeure de posséder des luminosités intrinsèques proches. Mieux encore, ces évènements ayant une durée typique de
quelques jours, leur courbe de luminosité est parfaitement observable. Pour les SN Ia, la forme de cette courbe, et plus particulièrement
la vitesse à laquelle elle décroit, permet de remonter encore plus précisément à leur luminosité intrinsèque maximale, comme
découvert en 1993
(M. M. Phillips
1993)
. Cela signifie que l'on peut connaitre leur magnitude absolue assez précisément sans connaitre leur distance !
Les supernovae Ia sont donc des "chandelles standard", à la manière des céphéides variables, mais leur importante luminosité
permet de mesurer des distances plus lointaines. Ce constat est supporté par des modélisations et il y a de bonnes raisons
d'avoir confiance en le potentiel des SN Ia en tant que chandelles standard.
Ainsi, observer la courbe de luminosité des SN Ia permet d'en déduire leur magnitude absolue et donc leur
distance de luminosité. On peut par ailleurs mesurer leur redshift. Or, la relation entre
distance de luminosité et redshift est fixée pour un modèle cosmologique donné.
Deux équipes sont alors formées pour recenser ces évènements et en déduire les paramètres de densité de notre Univers : la
High-Z Supernovae search team menée par Brian Schimdt et la Supernova Cosmology Project menée par Saul Perlmutter.
En 1998, les deux projets font part de leurs résultats
(Adam G. Riess, Alexei V. Filippenko
et al.
1998)
(S. Perlmutter, G. Aldering
et al.
1999)
, après étude d'une quarantaine de SN Ia. Ils parviennent ainsi à contraindre :
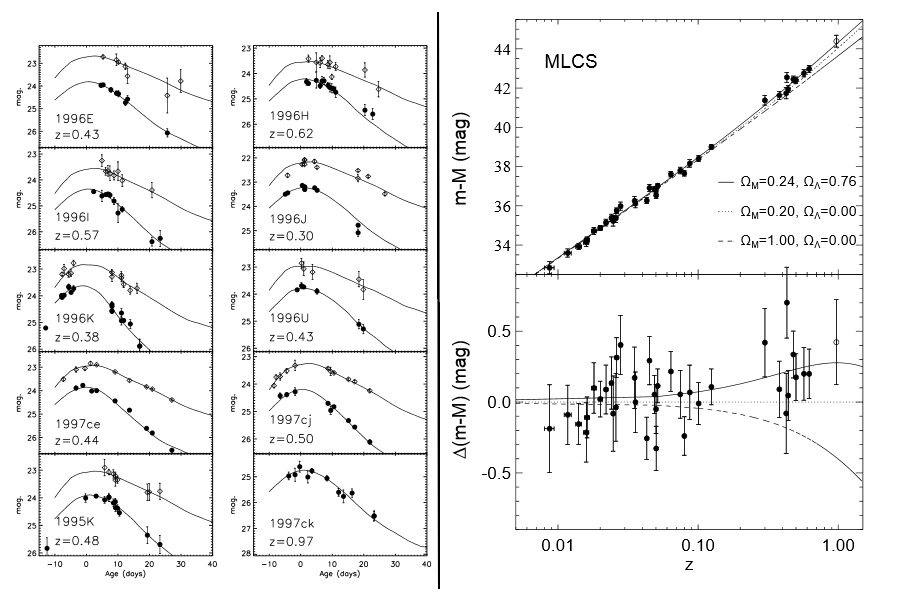
La conclusion est alors que l'Univers est incompatible avec une absence d'énergie du vide ou une
constante cosmologique nulle. Dans un Univers plat, les données indiquent $\Omega_m = 0,24$ et $\Omega_\Lambda = 0,76$ (L'Univers serait dominé
par l'
énergie du vide !) et que le
paramètre de décélération $q$ est strictement négatif. L'expansion de l'Univers accélère !
Cette découverte majeure est récompensée en 2011 par l'attribution du prix Nobel à Saul Perlmutter, Brian P. Schmidt
et Adam G. Riess.
En 1998 toujours, Dragan Huterer et Michael S. Turner introduisent le terme d'"énergie noire" (dark energy) (en référence
à la matière noire) pour désigner la forme d'énergie du vide invisible équivalente à une constante cosmologique
(Dragan Huterer, Michael S. Turner
1999)
.
La pression de dégénérescence d'un gaz d'électron est la pression de ces électrons du au principe d'exclusion de Pauli qui
en interdisant deux fermions d'être dans le même état quantique entraine que pour une pression donnée la densité d'électrons
ne peut dépasser une certaine valeur.