Au début des années 1990, le modèle le plus accepté parmi les cosmologistes est le modèle $S-CDM$, c'est-à-dire un Univers proche de sa densité de fermeture (plat) constitué en quasi totalité de matière noire froide, et également de matière baryonique froide. Ce modèle montre de plus en plus de faiblesses d'après les dernières observations, et de nouvelles données observationnelles sont nécessaires pour en comprendre les raisons.

Les supernovae sont des évènements consécutifs à la "mort" d'une étoile. Ils libèrent une énergie colossale et sont donc très lumineux. Au début des années 1990, on distingue deux catégories principales de supernovae (SN) :

• Les supernovae thermonucléaires (aussi appelées supernovae de type Ia) : Elles sont dues à l'effondrement de naines blanches (des étoiles compactes de masse proche de celle du Soleil mais de rayon 100 fois plus petit) maintenues en équilibre contre l'effondrement gravitationnel par la pression de dégénérescence de leurs électrons^[?]
• Les supernovae à effondrement de coeur : Elles sont dues à l'effondrement d'une plus grande variétés d'étoiles massives (masse supérieure à une dizaine de masses solaires) dès lors que leur coeur produit du Fer.

Les supernovae de type Ia se différencient des autres supernovae de type I par la présence de silicium dans leur spectre. Elles sont surtout comme propriété majeure de posséder des luminosités intrinsèques proches. Mieux encore, ces évènements ayant une durée typique de quelques jours, leur courbe de luminosité est parfaitement observable. Pour les SN Ia, la forme de cette courbe, et plus particulièrement la vitesse à laquelle elle décroit, permet de remonter encore plus précisément à leur luminosité intrinsèque maximale, comme découvert en 1993 (M. M. Phillips  1993) . Cela signifie que l'on peut connaitre leur magnitude absolue assez précisément sans connaitre leur distance ! Les supernovae Ia sont donc des "chandelles standard", à la manière des céphéides variables, mais leur importante luminosité permet de mesurer des distances plus lointaines. Ce constat est supporté par des modélisations et il y a de bonnes raisons d'avoir confiance en le potentiel des SN Ia en tant que chandelles standard. Ainsi, observer la courbe de luminosité des SN Ia permet d'en déduire leur magnitude absolue et donc leur distance de luminosité. On peut par ailleurs mesurer leur redshift. Or, la relation entre distance de luminosité et redshift est fixée pour un modèle cosmologique donné. Deux équipes sont alors formées pour recenser ces évènements et en déduire les paramètres de densité de notre Univers : la High-Z Supernovae search team menée par Brian Schimdt et la Supernova Cosmology Project menée par Saul Perlmutter. En 1998, les deux projets font part de leurs résultats (Adam G. Riess, Alexei V. Filippenko et al.  1998) (S. Perlmutter, G. Aldering et al.  1999) , après étude d'une quarantaine de SN Ia. Ils parviennent ainsi à contraindre :

• La constante de Hubble
• La densité de matière froide $\Omega_m$
• La densité d'énergie du vide $\Omega_\Lambda$ (équivalant à un terme de constante cosmologique)
• Le paramètre de décélération $q_0 = -\dot{H_0}/H_0^2-1$
• L'âge de l'Univers

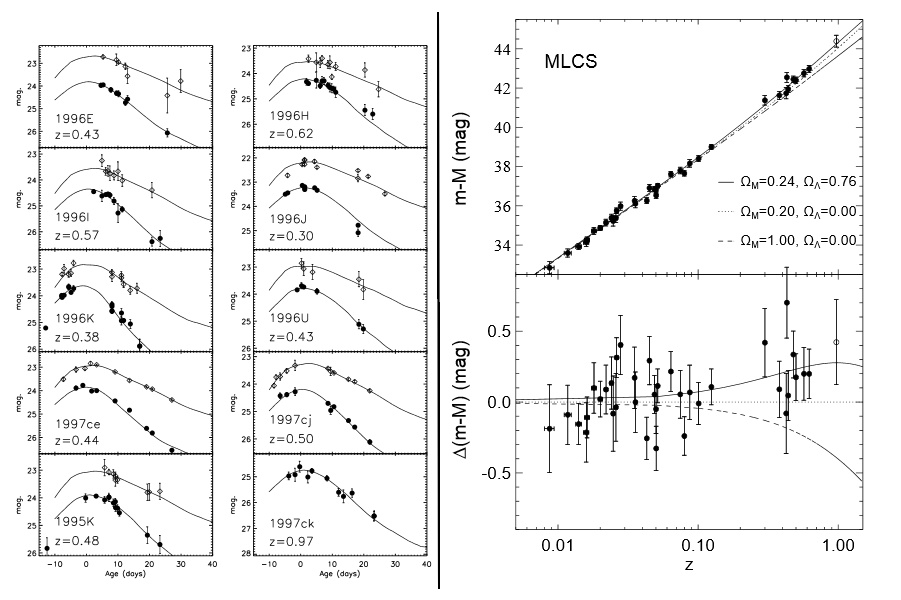
La conclusion est alors que l'Univers est incompatible avec une absence d'énergie du vide ou une constante cosmologique nulle. Dans un Univers plat, les données indiquent $\Omega_m = 0,24$ et $\Omega_\Lambda = 0,76$ (L'Univers serait dominé par l'énergie du vide !) et que le paramètre de décélération $q$ est strictement négatif. L'expansion de l'Univers accélère !

Cette découverte majeure est récompensée en 2011 par l'attribution du prix Nobel à Saul Perlmutter, Brian P. Schmidt et Adam G. Riess.

En 1998 toujours, Dragan Huterer et Michael S. Turner introduisent le terme d'"énergie noire" (dark energy) (en référence à la matière noire) pour désigner la forme d'énergie du vide invisible équivalente à une constante cosmologique (Dragan Huterer, Michael S. Turner  1999) .

La distance de luminosité d'une source irradiant de la lumière est la distance $d_L$ telle que le flux $F$ que l'on en reçoit est égal à : \begin{equation} F = \dfrac{L}{4\pi d_L^2} \end{equation} Où $L$ est la luminosité (en W) de la source. Cette grandeur est très utile en astronomie et a permis de grandes avancées en cosmologie. En effet, elle est accessible expérimentalement pour tous les objets dont on connait la magnitude absolue (ou luminosité intrinsèque), comme les céphéides ou les supernovas Ia. Pour de petites distances, la distance de luminosité est égale à la "distance" usuelle et cela en donne une mesure directe (c'est ainsi que furent mesurées les distances aux nébuleuses spirales et que fut découverte la loi de Hubble). Pour de grandes distances, dans un Univers en expansion, $d_L$ évolue de façon particulière : le redshift (décalage vers le rouge) et l'augmentation du temps de parcours de la lumière avec le temps diluent l'énergie de la source ; par ailleurs l'expansion affecte directement la taille du front d'onde lumineux. Pour un modèle cosmologique donné, on peut calculer la distance $d_L$ à partir du seul redshift $z$ d'un objet céleste. Or, le redshift $z$ est également accessible expérimentalement. Cela permet de contraindre ou rejeter des modèles d'expansion.

Calcul de $z \mapsto d_L(z)$

Soit une source $A$ comobile émettant $\Delta N$ photons de fréquence $\nu_e$ en un temps $\Delta t_e$ à partir de l'instant $t_e$. La puissance émise est alors $L = \dfrac{\Delta N}{\Delta t_e} h \nu_e$. On place un récepteur $B$ comobile à une distance comobile $\chi$ de $A$. L'onde lumineuse se propage et atteint sa cible au temps $t_r$. Le rayon du front d'onde est alors donné par : \begin{equation} l(\chi) = r(\chi) a(t_r) = a(t_r) S_k \left ( \displaystyle\int_{t_e}^{t_r} \dfrac{cdt}{a(t)} \right ) \end{equation} où : \begin{equation}\left\{\begin{matrix} S_k(\chi) & = & R \sin \dfrac{\chi}{R} \mbox{ si } k<0\\ S_k(\chi) & = & \chi \mbox{ si } k=0\\ S_k(\chi) & = & R \sinh \dfrac{\chi}{R} \mbox{ si } k>0 \end{matrix}\right.\end{equation} La surface du front d'onde vaut alors $4\pi l^2$. Les $\Delta N$ photons (leur nombre est conservé) sont reçus entre $t_r$ et $t_r + \Delta t_r$. Puisque le dernier et le premier photon ont parcouru la même distance comobile $\chi$ il vient que : \begin{equation} \chi = \displaystyle\int_{t_e}^{t_r} \dfrac{cdt}{a(t)} = \displaystyle\int_{t_e+\Delta t_e}^{t_r+\Delta t_r} \dfrac{cdt}{a(t)} \end{equation} Dans la limite où $\Delta t_e \to 0$ (on étudie le flux instantané de photons), alors en décomposant cette intégrale par relation de Chasles et en négligeant les variations de $a(t)$ on trouve : \begin{equation} \dfrac{\Delta t_r}{\Delta t_e} = \dfrac{a(t_r)}{a(t_e)} = 1+z \end{equation} Par ailleurs les photons qui arrivent en B ont subi un décalage spectral $z$ de même valeur si bien que leur fréquence à l'"arrivée" vérifie : \begin{equation} \dfrac{\nu_r}{\nu_e} = \dfrac{a(t_e)}{a(t_r)} = 1+z = \dfrac{\Delta t_r}{\Delta t_e} \end{equation} Finalement il vient donc que la puissance reçue sur la totalité du front d'onde est : \begin{equation} P = \dfrac{\Delta N}{\Delta t_r} h \nu_r = \dfrac{L}{(1+z)^2} \end{equation} Par ailleurs puisque le front d'onde a une surface $4\pi l^2$ il vient : \begin{equation} F = \dfrac{P}{4\pi l^2} = \dfrac{L}{4\pi \left ( l (1+z) \right ) ^2} \end{equation} De là : \begin{equation} d_L = (1+z) a(t_r) S_k \left ( \displaystyle\int_{t_e}^{t_r} \dfrac{cdt}{a(t)} \right ) \end{equation} Les observations que nous faisons sont réalisées à $t_r = 0$, donc : \begin{equation} d_L = (1+z) S_k \left ( \displaystyle\int_{t_e}^{0} \dfrac{cdt}{a(t)} \right ) \end{equation} On peut montrer à partir de l'équation de Friedmann que cette intégrale vaut, dans un Univers de poussière et d'énergie du vide : \begin{equation} \displaystyle\int_{t_e}^{0} \dfrac{cdt}{a(t)} = \displaystyle\int_{0}^{z} \dfrac{dz'}{H_0 \sqrt{\Omega_{\Lambda} + \left ( 1-\Omega_{\Lambda}-\Omega_m\right ) (1+z')^2 + \Omega_m (1+z')^3 }} \end{equation} Et : \begin{equation} d_L = (1+z) S_k \left (\displaystyle\int_{0}^{z} \dfrac{c dz'}{H_0 \sqrt{\Omega_{\Lambda} + \left ( 1-\Omega_{\Lambda}-\Omega_m\right ) (1+z')^2 + \Omega_m (1+z')^3 }} \right ) \end{equation} Pour un Univers plat cette expression se simplifie en : \begin{equation} d_L = (1+z) \dfrac{c}{H_0} \displaystyle\int_{0}^{z} \dfrac{dz'}{\sqrt{\Omega_{\Lambda} + \Omega_m (1+z')^3 }} \end{equation}

Comparaison entre modèles d'Univers

Dans le graphe ci-dessous, la relation $z\mapsto d_L(z)$ est calculée pour 3 modèles différents. Pour des valeurs suffisantes de $z$ les divergences permettent de contraindre les paramètres cosmologiques.

Découverte de l'accélération de l'expansion de l'Univers

La mesure de la relation distance de luminosité-redshift a permis en 1998 la découverte de l'accélération de l'expansion de l'Univers (voir ).

Les supernovas de type Ia constituent de bonnes chandelles standard. On connait donc à la fois leur magnitude absolue et apparente ce qui donne leur distance de luminosité $d_L$. Un fit est réalisé ci-dessous dans le cadre d'un Univers plat constitué de matière froide et d'énergie noire.