Au début des années 1990, le modèle le plus accepté parmi les cosmologistes est le modèle $S-CDM$, c'est-à-dire un Univers proche de sa densité de fermeture (plat) constitué en quasi totalité de matière noire froide, et également de matière baryonique froide. Ce modèle montre de plus en plus de faiblesses d'après les dernières observations, et de nouvelles données observationnelles sont nécessaires pour en comprendre les raisons.

Les supernovae sont des évènements consécutifs à la "mort" d'une étoile. Ils libèrent une énergie colossale et sont donc très lumineux. Au début des années 1990, on distingue deux catégories principales de supernovae (SN) :

• Les supernovae thermonucléaires (aussi appelées supernovae de type Ia) : Elles sont dues à l'effondrement de naines blanches (des étoiles compactes de masse proche de celle du Soleil mais de rayon 100 fois plus petit) maintenues en équilibre contre l'effondrement gravitationnel par la pression de dégénérescence de leurs électrons^[?]
• Les supernovae à effondrement de coeur : Elles sont dues à l'effondrement d'une plus grande variétés d'étoiles massives (masse supérieure à une dizaine de masses solaires) dès lors que leur coeur produit du Fer.

Les supernovae de type Ia se différencient des autres supernovae de type I par la présence de silicium dans leur spectre. Elles sont surtout comme propriété majeure de posséder des luminosités intrinsèques proches. Mieux encore, ces évènements ayant une durée typique de quelques jours, leur courbe de luminosité est parfaitement observable. Pour les SN Ia, la forme de cette courbe, et plus particulièrement la vitesse à laquelle elle décroit, permet de remonter encore plus précisément à leur luminosité intrinsèque maximale, comme découvert en 1993 (M. M. Phillips  1993) . Cela signifie que l'on peut connaitre leur magnitude absolue assez précisément sans connaitre leur distance ! Les supernovae Ia sont donc des "chandelles standard", à la manière des céphéides variables, mais leur importante luminosité permet de mesurer des distances plus lointaines. Ce constat est supporté par des modélisations et il y a de bonnes raisons d'avoir confiance en le potentiel des SN Ia en tant que chandelles standard. Ainsi, observer la courbe de luminosité des SN Ia permet d'en déduire leur magnitude absolue et donc leur distance de luminosité. On peut par ailleurs mesurer leur redshift. Or, la relation entre distance de luminosité et redshift est fixée pour un modèle cosmologique donné. Deux équipes sont alors formées pour recenser ces évènements et en déduire les paramètres de densité de notre Univers : la High-Z Supernovae search team menée par Brian Schimdt et la Supernova Cosmology Project menée par Saul Perlmutter. En 1998, les deux projets font part de leurs résultats (Adam G. Riess, Alexei V. Filippenko et al.  1998) (S. Perlmutter, G. Aldering et al.  1999) , après étude d'une quarantaine de SN Ia. Ils parviennent ainsi à contraindre :

• La constante de Hubble
• La densité de matière froide $\Omega_m$
• La densité d'énergie du vide $\Omega_\Lambda$ (équivalant à un terme de constante cosmologique)
• Le paramètre de décélération $q_0 = -\dot{H_0}/H_0^2-1$
• L'âge de l'Univers

La conclusion est alors que l'Univers est incompatible avec une absence d'énergie du vide ou une constante cosmologique nulle. Dans un Univers plat, les données indiquent $\Omega_m = 0,24$ et $\Omega_\Lambda = 0,76$ (L'Univers serait dominé par l'énergie du vide !) et que le paramètre de décélération $q$ est strictement négatif. L'expansion de l'Univers accélère !

Cette découverte majeure est récompensée en 2011 par l'attribution du prix Nobel à Saul Perlmutter, Brian P. Schmidt et Adam G. Riess.

En 1998 toujours, Dragan Huterer et Michael S. Turner introduisent le terme d'"énergie noire" (dark energy) (en référence à la matière noire) pour désigner la forme d'énergie du vide invisible équivalente à une constante cosmologique (Dragan Huterer, Michael S. Turner  1999) .

Une céphéide est une étoile variable périodique, c'est-à-dire dont la luminosité diminue et augmente de façon stable et périodique. Il existe plusieurs types de céphéides. Les céphéides classiques dites de Classe I sont très lumineuses (jusqu'à 100 000 fois plus que le Soleil !) ce qui les rend visible individuellement même à très grande distance.

Usage en tant que chandelle standard

La luminosité intrinsèque (c'est-à-dire la puissance rayonnée) des céphéides présente la particularité de ne dépendre que de leur période de variation lumineuse (la relation dépendant en revanche du type de céphéide dont il s'agit). Or, le flux reçu par unité de surface à une distance $d$ d'une source lumineuse est égal à $\Phi = L/(4\pi d^2)$ où $L$ est sa luminosité. En observant une céphéide, on connait à la fois $L$ par le biais de sa période $T$ facilement observable (de l'ordre de grandeur de la journée) et d'autre part la puissance reçue par unité de surface. Cela donne donc la distance $d = \sqrt{\dfrac{L}{4 \pi \Phi}}$. On appelle de tels objets, pour lesquel la luminosité intrinsèque est connue, des "chandelles standards".

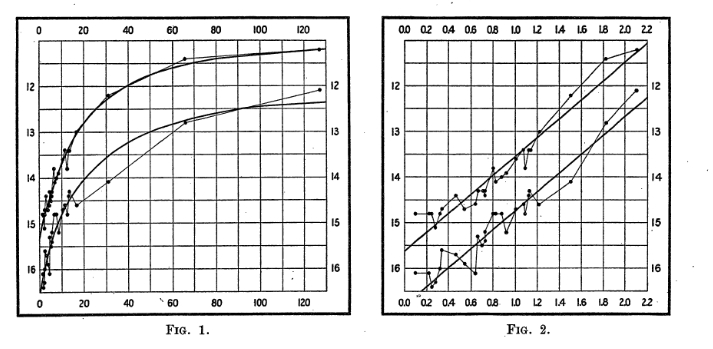
Découverte de la relation luminosité-période : La découverte de l'existence d'une relation entre luminosité et période des céphéides et due à Henrietta Leavitt. En 1908, cette astronome de l'observatoire de l'université d'Harvard étudie des milliers d'étoiles variables pulsantes appartenant aux nuages de Magellan (deux galaxies naines environ 20 fois plus proches de la Voie Lactée qu'Andromède) et mesure leur magnitude apparente (grandeur plus pratique en Astronomie pour représenter la brillance que le flux lumineux en $W/m^2$) et leur période. Elle suppose alors que toutes les étoiles d'un "nuage" sont approximativement à la même distance de la Terre, ce qui entraine que la différence entre leur magnitude apparente et absolue (qui ne dépend que de la distance entre elles et la Terre) est une constante : $m-M = C$. Elle remarque que la magnitude apparente de certaines de ces étoiles variables est une fonction de leur période, autrement dit, $m_{magellan} = m_{magellan}(T)$.

Cependant, ce n'est pas suffisant pour mesurer des distances. En effet, ceci requiert de connaitre la luminosité intrinsèque ou encore la magnitude absolue en fonction de la période, sans quoi la relation ainsi obtenue ne permet d'évaluer que le rapport entre la distance d'une céphéide avec la distance de celles qui ont permis d'établir cette relation (qui est inconnue). Il faut alors attendre les travaux de Hertzsprung et Shapley dans les années qui suivent pour étalonner cette relation et obtenir la courbe de la magnitude absolue cette fois. Pour cela, ces astronomes ont mesuré la magnitude et la période d'une céphéide proche dont la distance était connue (par la méthode de la parallaxe). Ils ont ainsi pu calculer sa magnitude absolue $M$. En reportant cette mesure dans la courbe de Leavitt, ils ont pu déterminer quelle était la constante $C$ qui séparait $m_{magellan}$ et $M$. De là ils en ont déduit la loi $T\mapsto M(T)$.

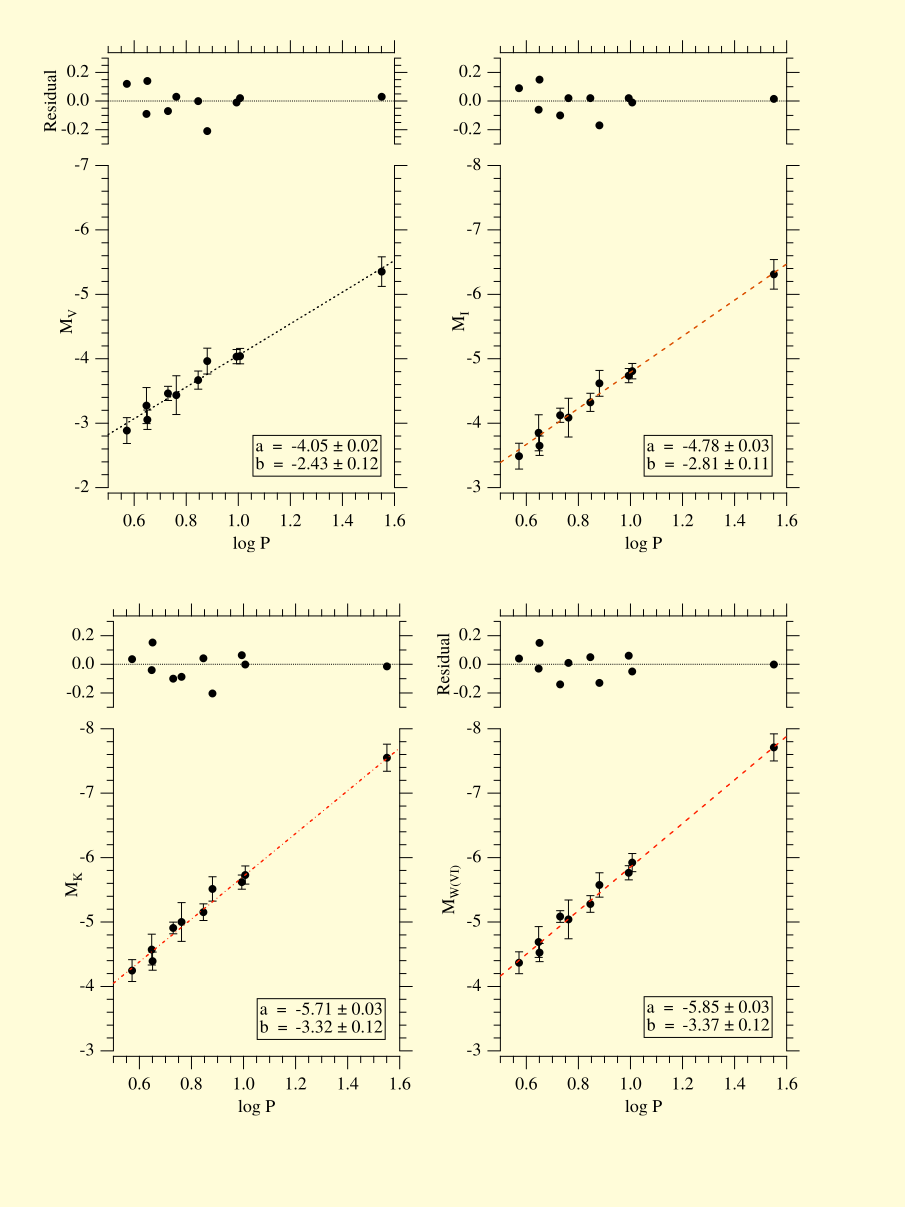
Les mesures du téléscope spatial Hubble pour 10 céphéides proches établissent la relation suivante entre la magnitude absolue dans la bande V et la période $P$ en jours (G. Fritz Benedict, Barbara E. McArthur et al.  2007) : \begin{equation} M_V = \left (-\mbox{2,43} \pm \mbox{0,12} \right) \left ( \log P - 1 \right) - \mbox{4,05} \pm \mbox{0,02} \end{equation} Cette relation implique une relation de forme loi de puissance entre la luminosité intrinsèque $L$ et la période $P$, de la forme $L \propto P^{1+\epsilon}$.

La relation entre période et magnitude absolue n'est pas tout à fait univoque, probablement parce que d'autres paramètres peuvent différer d'une céphéide variable à une autre avec un impact relativement faible. Ceci limite le pouvoir prédictif de la relation luminosité période de $\Delta M_{V} \sim $ 0,1 (L. N. Berdnikov, A. K. Dambis et al.  1997) .

Cette méthode a permis de mesurer des distances de galaxies hôtes jusqu'à environ 30 Mpc (Jeffrey A. Newman, Stephen E. Zepf et al.  1999) (Adam G. Riess, Weidong Li et al.  2005)

Explication théorique par Eddington :

Découverte d'une nouvelle classe de céphéides :