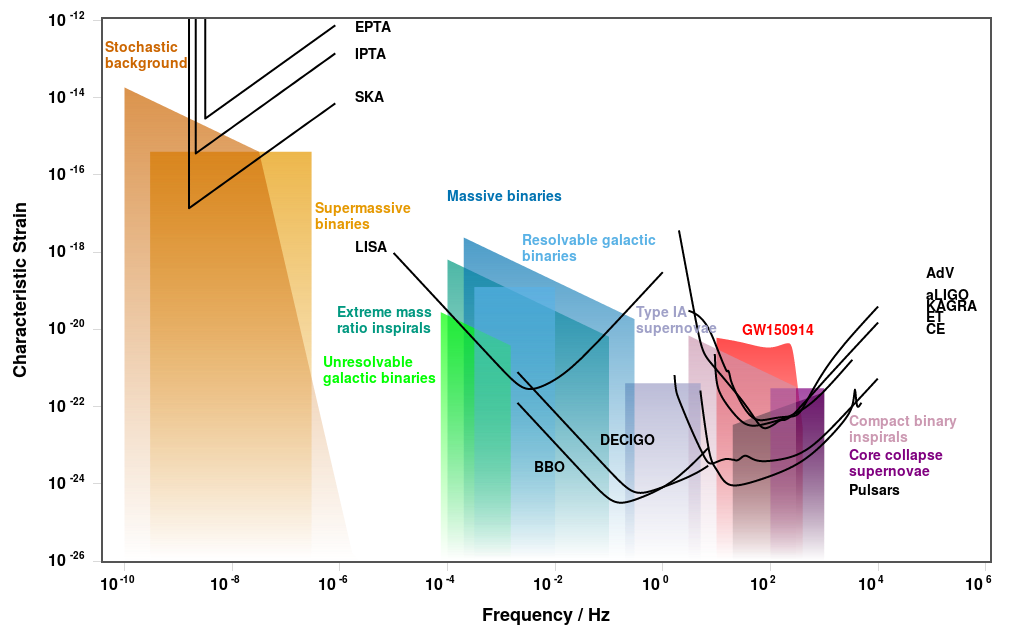
Prédiction et caractéristiques

Les ondes gravitationnelles sont une prédiction établie par Einstein en 1916 en tant que conséquence de la relativité générale. Ce sont une solution particulière des équations d'Einstein qui se traduisent par la propagation à la vitesse de la lumière d'une perturbation de l'espace-temps, sous la forme d'une onde transverse d'amplitude généralement notée $h$. Un objet de longueur au repos $L$ voit ainsi varier sa longueur de $\pm hL$.

Une distribution de masse accélérée dissymétrique émet des ondes gravitationnelles : c'est le cas par exemple de systèmes binaires d'étoiles ou de trous noirs, d'étoiles à neutrons oscillantes, ou encore de supernovae. Émises par ces ondes distances, ces sources se propagent jusqu'à la Terre, leur amplitude décroissant en $1/r$. Pour un système binaire de deux masses $M$ séparées d'une distance $a$ et situées à une distance $r$ de la Terre, l'ordre de grandeur de l'amplitude de la perturbation $h$ est donné par (B. F. Schutz  1997) : \begin{equation} h \sim \frac{G^2}{c^4}\dfrac{M^2}{ar} \end{equation} Si $M \sim 10 M_{\odot}$ et $a$ est de l'ordre de 10 fois le rayon de Schwarzschild associé à $M$, et que le système est distant de 100 Mpc de la Terre, alors : \begin{equation} h \sim 10^{-54} \times \dfrac{10^{62}}{10^{5} \times 10^{24}} \sim 10^{-21} \end{equation} Le facteur $1/r$ est la décroissance de l'amplitude avec la distance. Le préfacteur $G^2/c^4$ vaut environ $10^{-54} \textrm{kg}^{-2}.\textrm{m}^{2}$. La faiblesse de sa valeur numérique explique la petitesse de $h$. L'onde émise par ce système traversant la terre ne déforme un objet d'un mètre que d'une longueur de $10^{-21}$ m ! Une des conséquences de cette émission d'ondes gravitationnelles est qu'un système binaire de cette sorte perd de l'énergie. Ainsi, deux étoiles en orbite l'une autour de l'autre de demi-grand axe $a$ suffisamment faible (avec une rotation rapide selon la loi de Kepler $T^2 \propto a^3$ et donc fortement accélérées) tendront à se rapprocher jusqu'à fusionner puisqu'en perdant de l'énergie les masses se rapprochent ($a \propto -1/E$). L'onde gravitationnelle émise est essentiellement de fréquence $f_{OG} \sim 2 f_{rot} \sim \dfrac{(GM)^{1/2}}{2\pi a^{3/2}}$. En utilisant les valeurs précédentes, on obtient $f_{OG} \sim $ 1000 Hz.

Première observation indirecte

En 1974, Russel Hulse et Joseph Taylor découvrent le pulsar binaire "PSR B1913+16" (R. A. Hulse, J. H. Taylor  1975) composé a priori d'une étoile à neutron émettant dans notre direction avec une période de rotation 59 millisecondes et d'un compagnon compact, a priori une autre étoile à neutron. Ils mesurent entre autres le demi-grand axe du système ($2\times 10^{6}$ km) et sa période orbitale (27 900 s environ). En 1975 Robert Wagoner suggère que puisque d'après la relativité générale un tel système perd une quantité significative d'énergie par émission d'ondes gravitationnelles, alors son demi-grand axe doit diminuer et sa période orbitale aussi dans des proportions mesurables (R. V. Wagoner  1975) . Ce système permettrait donc de tester la réalité des ondes gravitationnelles. En 1979, Joseph Taylor donne les résultats de cette mesure de $\dot{T}$ (le taux de diminution de la période) et trouve $\dot{T}^{obs}/\dot{T}^{th} = 1,3 \pm 0,3$ (J. H. Taylor, L. A. Fowler et al.  1979) (Thibault Damour  2015) , confirmant ainsi de façon assez convaincante l'existence des ondes gravitationnelles.

Depuis, les données ont été accumulées et ont permis de contrôler l'écart entre la prédiction de la relativité générale et l'observation à moins de 0,2 $\%$.

En 1993, R. Hulse et J. Taylor ont reçu le prix Nobel pour leur découverte de ce pulsar qui a permis de tester précisément la relativité générale.

Les détecteurs interférométriques LIGO et VIRGO

Au début des années 1970, Rainer Weiss travaille au MIT sur la possibilité de détecter des ondes gravitationnelles à l'aide d'un interféromètre de type michelson éclairé par un laser, en étudiant les différentes sources de bruit potentielles. Un tel détecteur repose sur le principe suivant : lors du passage d'une onde gravitationnelle, la métrique est perturbée différemment dans des directions perpendiculaires. En entrant dans un interféromètre de Michelson, celle-ci affecte donc la longueur $L$ de ses deux bras perpendiculaires. La différence de longueur induite $\delta L$ modifie la figure d'interférences en sortie de l'interféromètre, rendant détectable le passage de l'onde. Pour une configuration optimale^[?], la variation de longueur est de : \begin{equation} \delta L = \dfrac{1}{2} h L \end{equation} Comme on l'a vu, $h$ est très petit, ce qui rend cette variation très difficile à mesurer. L'objectif est donc d'obtenir des bras aussi longs que possible.

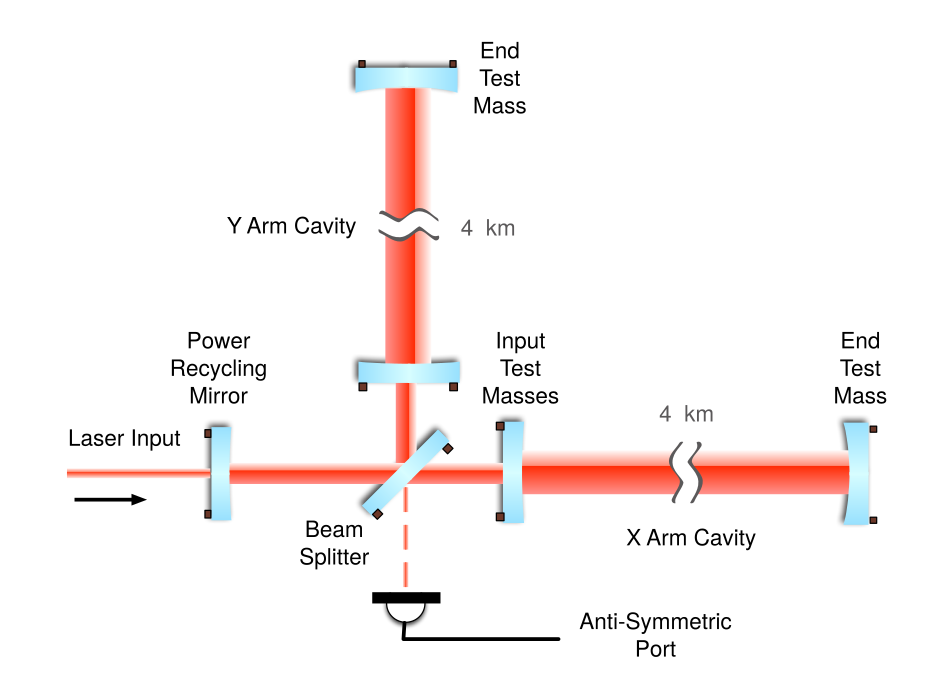
Parallèlement, à Caltech, Kip Thorne et son équipe travaillent sur les sources astrophysiques d'ondes gravitationnelles et le potentiel de détection par une expérience du type de celle envisagée par Weiss. Deux projets expérimentaux sont alors lancés, celui du MIT mené par Weiss, celui de Caltech mené par Ronald Drever et Stan Whitcomb. Des prototypes de petite taille sont conçus et la faisabilité d'un détecteur de plusieurs kilomètres est envisagée. En 1984 Caltech et le MIT unissent leurs efforts et conçoivent le projet LIGO de détecteur interférométrique avec des bras de plusieurs kilomètres de long.

Le projet LIGO est validé au début des années 1990 et 3 détecteurs sont construits, deux dans la même enceinte à Hanford, Washington, et pourvus de bras de 4 et 2 km ("H1" et "H2"), et un a Livingstone, Louisiane ("L1", avec des bras de 4 km). La construction prend fin en 2002. Des prises de données sont effectuées jusqu'en 2010, sans détection confirmée. Le projet aLIGO (advanced LIGO) validé au début des années 2000 est alors implémenté entre 2010 et 2014. En 2015, la sensibilité des détecteurs a été largement améliorée, et les prises de données recommencent. Le 14 septembre 2015, les détecteurs LIGO observent simultanément une onde gravitationnelle émise par la coalescence de deux trous noirs à une distance 400 Mpc, réalisant ainsi la première détection directe d'une telle onde (B. P. Abbott, R. Abbott et al.  2016) . L'événement est baptisé GW150914. Cette découverte sera récompensée par l'attribution du prix Nobel de Physique 2017 à Barry Barish, Kip Thorne et Rainer Weiss. À ce jour (3 octobre 2017), LIGO a observé quatre trains d'ondes gravitationnelles, à chaque fois provenant de systèmes binaires de trous noirs en rotation.

Parallèlement au développement de LIGO aux États-Unis, le projet d'un interféromètre européen est lancé au milieu des années 1990 par le CNRS et l'INFN. Construit non loin de Pise, des prises de données ont été effectuées entre 2007 et 2011, sans qu'un événément ne sont détecté. Un projet d'amélioration visant à augmenter la sensibilité de l'expérience est alors entrepris (Advanced Virgo) avec pour objectif de nouvelles prises de données dès fin 2016. Le fonctionnement concurrentiel de plusieurs détecteurs permet de mieux reconstruire la direction de la source par triangulation, et donc de chercher la présence de signaux complémentaires (lumière, neutrinos) dans cette direction. Le 14 août 2017, Virgo réalise sa première détection cojointe avec LIGO ( The LIGO Scientific Collaboration, the Virgo Collaboration et al.  2017) . Les données de Virgo ont permis, pour cet événement, de réduire la zone de confiance à 90 % de la position dans le ciel de la source de 1160 $\textrm{deg}^2$ à 60 $\textrm{deg}^2$.

Le 17 août 2017, LIGO et Virgon détectent, pour la première fois, la phase finale de la fusion de deux étoiles à neutrons (B. P. Abbott, R. Abbott et al.  2017) (B. P. Abbott, R. Abbott et al.  2017) . Plusieurs instruments ont détecté incidemment un sursaut gamma (GRB 170817A) ayant survenu 1,7 s après l'instant de fusion mesuré par LIGO-Virgo. Cette découverte marque une nouvelle ère dans l'astronomie multi-messagers : dans ce cas, l'observation conjointe des ondes gravitationnelles et de la lumière émise par la source a permis, entre autre, l'identification de la galaxie hôte (NGC 4993) dont le redshift $z$ est connu avec une bonne précision. Or, l'objet étant relativement proche (par rapport à la taille de l'Univers), la relation de Hubble s'applique et $z = H_0 d / c$. Par ailleurs, LIGO donne une mesure indépendante de $d$, et cela permet donc d'en déduire une estimation de la constante de Hubble évaluée à $H_0 = 70.0\substack{+12.0 \\ -8.0}$ (B. P. Abbott, R. Abbott et al.  2017) . C'est la première application cosmologique concrète effectuée grâce aux ondes gravitationnelles.

Limitations et prochaines générations de détecteurs

Sources de bruit

La sensibilité des détecteurs actuels est limitée à basse fréquence ($\sim$ Hz) par le bruit sismique et à haute fréquence (kHz) par le bruit d'origine quantique, qui est la somme du bruit de grenaille (shot noise) et du bruit du aux fluctuations de pression de radiation des photons. Ils dépendent de la pression $P$ du Laser, de la longueur $L$ des bras et de la masse $M$ des miroirs de la façon suivante : \begin{equation} \tilde{h}_{grenaille} = \dfrac{1}{4\pi L} \sqrt{\dfrac{2h\lambda c}{\eta P}} \mbox{ et } \tilde{h}_{pression} = \dfrac{1}{ML}\sqrt{\dfrac{hP}{2\pi^4 c\lambda}} \dfrac{1}{f^2} \end{equation} Varier la puissance d'un laser permet d'effectuer un trade-off entre bruit de grenaille et bruit de recul, et éventuellement d'optimiser la sensibilité pour certaines fréquences, mais pas plus. En revanche, le bruit quantique étant inversement proportionnel à $L$, il peut être supprimé à l'aide de plus longs bras.

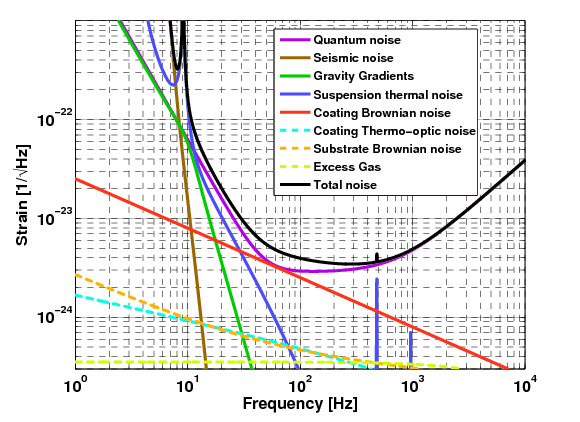
Futurs détecteurs

Pour dépasser ces limitations, les futurs détecteurs se répartiront en deux catégories :

• Les détecteurs dans l'espace, qui s'affranchiront ainsi du bruit sismique et seront sensibles à des ondes gravitationnelles de basse fréquence. C'est notamment le cas de LISA, dont les trois détecteurs seront distants de 2,5 millions de km et seront sensibles à des fréquences entre $10^{-4}$ et $10^{-1}$ Hz. D'autres expériences sont à l'étude, comme BBO (Big Bang Observer) et DECIGO (DECi-hertz Interferometer Gravitational wave Observatory) avec des bras de 10 000 à 50 000 km et 1 000 km de long respectivement. En effet, la sensibilité de LISA à certaines sources risque serait limitée par du bruit de confusion (c'est-à-dire la superposition de signaux impossible à résoudre individuellement) dans la zone des très basses fréquences (Leor Barack, Curt Cutler  2004) . Cette limite « fondamentale » suggère d'explorer des intervalles de fréquences plus élevées, intermédiaires entre celui de LISA et ceux des détecteurs terrestres actuels ou futurs. Ces détecteurs ne pouvant résoudre des ondes de longueur d'onde bien plus courte que leurs bras, ceux-ci sont nécessairement plus courts.
• Les détecteurs terrestres de troisièmes génération qui s'affranchiront du bruit quantique au moyen de bras plus longs, tels que le Einstein Telescope (10 km) ou le Cosmic Explorer (40 km). Ils pourront aussi être placés plus en profondeur pour contrôler le bruit sismique. L'Einstein Telescope diffère des détecteurs terrestres actuels par sa géométrie triangulaire.

Perspectives

Sources potentielles

De façon générale, la détection d'ondes gravitationnelles offre une fenêtre d'observation indépendante du canal électromagnétique habituel et permet d'accéder à une grande variété de phénomènes. Plusieurs recherches sont ainsi effectuées par LIGO :

• Coalescence d'objets compacts : Recherche de fusions de systèmes binaires d'objects compacts (trou-noir/trou-noir, étoile à neutron/trou-noir, étoile à neutron/étoile à neutron). Ceci permet de mesurer leurs masses initiale, la masse de l'objet final, leur distance de luminosité et redshift.
• Supernovae à effondrement de coeur : Recherche d'ondes gravitationnelles en coincidence avec des supernovae à effondrement de coeur, afin de mieux comprendre les mécanismes en jeu. La signature gravitationnelle de ces événements est mal comprise et difficile à modéliser, et ces observations seraient très précieuses. On considère que les détecteurs actuels ne sont capables de détecter ces supernovae que dans la Voie Lactée et les nuages de Magellan, où elles surviennent à un taux de l'ordre d'une fois par siècle. Seules les prochaines générations de détecteurs ont donc des chances réalistes d'effectuer de telles détections.
• Fond stochastique : Recherche d'un fond stochastique d'origine cosmologique, tel que motivé par certaines théories comme la théorie des cordes (Xavier Siemens, Vuk Mandic et al.  2007) .

Cosmologie

La détection de sources transitoires comme les coalescences d'objets compacts permet d'accéder à leur distance de luminosité. Les futures générations de détecteurs devraient permettre non seulement d'observer ces événements à des échecs cosmologiques ($z>1$), comme des coalescences de systèmes d'étoiles à neutrons y compris pendant la réionisation ($z \sim 6$), mais aussi la totalité des coalescences de trous noirs tels que $M \gtrsim 30 M_{\odot}$ dans l'univers observable (attendus jusqu'à $z \sim 10$) (B. P. Abbott, R. Abbott et al.  2016) . En principe, pour des événements de ce type, le redshift n'est pas mesurable facilement ou directement, à cause de ce qu'on appelle la dégénérescence masse-redshift. La conséquence de celle-ci est qu'on ne peut extraire que $M(1+z)$ à partir de la forme du signal (où $M$ est la masse au repos). Il existe cependant des méthodes imprécises (erreur de 10-20$\%$ sur $z$) pour remonter au redshift dans certains cas (C. Messenger, Kentaro Takami et al.  2014) . Heureusement, des signaux électromagnétiques détéctables peuvent être associés avec ces événements comme ce fut observé pour la première fois avec GW170817, permettant ainsi une mesure indépendante et précise de $z$. Il est donc en théorie possible de vérifier par cette méthode indépendante les résultats obtenus à partir des supernovae thermonucléaires en tant que chandelles standards via la relation $z \mapsto d_L(z)$.

En principe, les détecteurs sont capables de détecter un fond stochastique si un excès significatif de densité d'énergie est observé dans une certaine plage de fréquence. Comme les photons libérés au découplage vers $T \sim $ 3000 K, des ondes gravitationnelles produite dans les premiers instants de l'Univers ont pu être libérées par un découplage qu'on peut estimer avoir survenu à une température inférieur à la température de Planck ($10^{19}$ GeV). Elles pourraient donc contenir de la l'information sur la physique à très haute énergie. Les détecteurs seraient capables de mesurer un paramètre de densité $\Omega_{GW}(f)$ défini à partir de la densité d'énergie d'ondes gravitationnelles selon : \begin{equation} \Omega_{GW}(f) = \dfrac{1}{\rho_c} \dfrac{d\rho_{Gw}}{d\log f} \end{equation} Par exemple, les modèles d'inflation les plus simples prédisent un fond stochastique... (TODO)

Une supernova de type Ia (thermonucléaire) est le phénomène très lumineux d'explosion d'une naine blanche lorsque celle-ci en accrétant de la matière devient trop massive pour demeurer stable. Les supernovae Ia sont très intéressantes en cosmologie, car ce sont des chandelles standard, similairement aux céphéides. Elles permettent donc d'effectuer des mesures de distance de luminosité. Étant très lumineuses, elles sont détectables même étant lointaines, jusqu'à des redshift dépassant 1. Or, à ces redshift, la dépendance de la distance de luminosité avec le redshift dépend beaucoup du modèle cosmologique, et donc les supernovae permettent de mesurer assez précisément des paramètres cosmologiques. C'est par leur étude que fut découverte l'accélération de l'expansion de l'Univers.

Cette annexe est divisée en trois parties :

• Naines blanches et masse de Chandrasekhar
• Effondremment
• Emploi comme chandelles standards

Les naines blanches, masse de Chandrasekhar

Les naines blanches sont des étoiles très compactes ($m\sim M_{\odot}$ et $R \sim 1\% \cdot R_{\odot}$), principalement constituées de carbone et d'oxygène, qui ne résistent à l'effondrement gravitationnel non pas par des réactions thermonucléaires en leur sein puisque celles-ci ne sont plus prédominantes, mais grâce à la pression de dégénérescence de leurs électrons, d'origine quantique. La suite de ce paragraphe consiste à montrer l'existence d'une masse limite pour ces objets, appelée masse de Chandrasekhar, au-delà de laquelle cette pression de dégénérescence est insuffisante pour soutenir le poids de la naine blanche.

Equation d'état du gaz d'électrons

On considère l'ensemble des électrons qui constituent l'étoile. Ceux-ci sont confinés à d'importantes pressions et densités, et leur comportement est à la fois quantique et relativiste. On cherche à établir l'équation d'état du gaz d'électrons. Pour les décrire, on apparente le système qu'ils forment à une boite de dimension $L\times L \times L$ remplie d'électrons. Pour commencer, il faut déterminer les différents états microscopiques autorisés. Pour cela on résout l'équation de Dirac (pour conserver une description quantique et relativiste), en considérant que les électrons ne peuvent s'échapper de la boite (fonction d'onde nulle aux bords) : \begin{equation} i\hbar \gamma^\mu \partial_\mu \psi - mc \psi = 0 \mbox{ et } \psi (t, \vec{x}) = 0 \mbox{ si } x_i \in \{ 0, L \} \end{equation} En recherchant les solutions sous formes d'ondes on trouve : \begin{equation} \psi (t,\vec{x}) = \begin{pmatrix} \phi\\ \left [ \dfrac{\vec{\sigma} \vec{p}}{E+mc^2} \right ] \phi \end{pmatrix} e^{\frac{i}{\hbar}\left( Et - \vec{p} \cdot \vec{x}\right )} \end{equation} où $E = +\sqrt{m^2c^4 + p^2c^2}$, l'expression relativiste de l'énergie. L'application des conditions aux limites donne $p_i = h n_i / L$ avec $n_i \in \mathbb{Z}$. (Même résultat avec l'équation de Schrodinger, donc non relativiste). Maintenant que l'on connait l'ensemble des micro-états, la question est de connaitre les grandeurs thermodynamiques que sont la densité, la densité d'énergie et la pression et de les relier. On définit la fonction $f_i(E_i)$ définie comme le nombre d'électrons dans l'état $i$. Les électrons étant des fermions, pour un équilibre thermique, ils suivent la distribution de Fermi-Dirac. Ainsi, le nombre d'électrons $n_i$ dans un état $i$ est dans ce cas donné par : \begin{equation} f_i(E_i) = \dfrac{g}{e^{E_i/k_B T} + 1} \end{equation} Où $g$ est la dégénérescence de spin (pour un spin 1/2 comme c'est le cas pour les électrons, $g=2$). Ici, chaque état est déterminé par les nombres quantique $n_x,n_y,n_z$ tels que $p^2 = \frac{h^2}{L^2} (n_x^2 + n_y^2 + n_z^2)$. Le nombre $N$ d'électrons est donné par la somme des espérances moyennes associées à chaque état : \begin{equation} N = f_i(E_i) = g \sum_{n_x = -\infty}^{+\infty} \displaystyle \sum_{n_y = -\infty}^{+\infty} \displaystyle \sum_{n_z = -\infty}^{+\infty} f \left (E(n_x, n_y, n_z)\right ) \end{equation} Remarquons que les niveaux d'impulsions (et donc d'énergie) sont de moins en moins espacés quand $L\to +\infty$, si bien que l'écart entre deux niveaux consécutifs devient infinitésimal. On peut donc transformer les sommes en intégrales selon :^[?] \begin{equation} \sum_{n_x = -\infty}^{+\infty} \to \dfrac{L}{h} \displaystyle\int_{-\infty}^{+\infty} dp_x \end{equation} L'expression du nombre d'électrons $N$ devient alors : \begin{equation} N = g\dfrac{L^3}{h^3} \displaystyle\int_{-\infty}^{+\infty} \displaystyle\int_{-\infty}^{+\infty} \displaystyle\int_{-\infty}^{+\infty} f \left (E(p_x, p_y, p_z)\right ) dp_x dp_y dp_z \end{equation} L'intégrande ne dépendant que de $E$ qui ne dépend que de la norme de $\vec{p}$ (pas de sa direction), il est intéressant de passer en coordonnées sphériques : \begin{equation} N = g\dfrac{L^3}{h^3} \displaystyle\int_{\theta = 0}^{2\pi} \displaystyle\int_{\phi = 0}^{\pi} \displaystyle\int_{p = 0}^{+\infty}p^2 \sin{(\phi)} f(E(p))dp \\ = 4\pi g\dfrac{L^3}{h^3} \displaystyle\int_{0}^{+\infty} f(E(p)) p^2 dp \end{equation} Enfin, la densité d'électrons $n$ vaut simplement $N/L^3$ et donc : \begin{equation} n =\dfrac{ 4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} f(E(p)) p^2 dp \end{equation} L'énergie totale du système $U$ est donnée par la somme des énergies moyennes de chaque état $U_i = f_i E_i$. En sommant sur tous les états autorisés on trouve : \begin{equation} U = g \displaystyle \sum_{n_x = -\infty}^{+\infty} \displaystyle \sum_{n_y = -\infty}^{+\infty} \displaystyle \sum_{n_z = -\infty}^{+\infty} f \left (E(p_x, p_y, p_z)\right ) E(n_x, n_y, n_z) \end{equation} Cette somme peut être transformée en intégrale par le même processus de continuisation que précédemment. La seule différence est la présence d'un facteur $E$ supplémentaire dans l'intégrale : \begin{equation} U = 4\pi g\dfrac{L^3}{h^3} \displaystyle\int_{0}^{+\infty} f \left (E(p)\right ) E(p) p^2 dp \end{equation} La densité d'énergie est simplement $\rho = U/L^3$, et donc : \begin{equation} \rho = \dfrac{4\pi g}{h^3} \displaystyle\int_{0}^{+\infty}f \left (E(p)\right ) E(p) p^2 dp \end{equation} La pression des électrons d'impulsion $p$ est $pv/3$ ^[?] Par ailleurs $v = pc^2/E$. ^[?] De là : \begin{equation} P = \dfrac{4\pi g}{3h^3} \displaystyle\int_{0}^{+\infty}f \left (E(p)\right ) \dfrac{p^4 c^2}{E(p)} dp \end{equation} Si les électrons sont à l'équilibre thermique, ils suivent la distribution de fermi-dirac et donc : \begin{equation}\left\{\begin{matrix} n & = & \dfrac{ 4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} \dfrac{p^2 dp}{e^{E(p)/k_B T} + 1}\\ \rho & = & \dfrac{4\pi g}{h^3} \displaystyle\int_{0}^{+\infty} \dfrac{p^2 E(p) dp}{e^{E(p)/k_B T} + 1} \\ P & = & \dfrac{4\pi g}{3h^3} \displaystyle\int_{0}^{+\infty} \dfrac{1}{E(p)} \dfrac{p^4 c^2 dp}{e^{E(p)/k_B T} + 1} \end{matrix}\right.\end{equation} Les intégrales peuvent être réécrites à l'aide des variables $u = E/mc^2 = 1+\frac{p^2}{m^2c^2}$ et $x = mc^2/(k_B T)$ : \begin{equation}\left\{\begin{matrix} n & = & \dfrac{ 4\pi g m^3 c^3}{h^3} \displaystyle\int_{1}^{+\infty} \dfrac{u \sqrt{u^2-1} du}{e^{ux} + 1}\\ \rho & = & \dfrac{4\pi g m^4 c^5}{h^3} \displaystyle\int_{1}^{+\infty} \dfrac{u^2 \sqrt{u^2-1} du}{e^{ux} + 1} \\ P & = & \dfrac{4\pi g m^4 c^5}{3h^3} \displaystyle\int_{1}^{+\infty} \dfrac{(u^2-1)^{3/2} du}{e^{ux} + 1} \end{matrix}\right.\end{equation} On s'intéresse ici à l'équation d'état $n \to P (n)$ puisque la relation nécessaire à la résolution du problème est celle entre la densité de masse d'électrons $\rho_m = n m$ et la pression $P$. Les intégrales peuvent être évaluées numériquement. Si les effets thermiques ne dominent plus, un cas extrême à envisager est le cas où tous les niveaux en dessous d'une certaine énergie de seuil $E_F$ sont occupé. On parle d'état dégénéré. Ceci permet de maximiser la densité d'électrons à une énergie totale donnée. Dans ce cas la fonction $f(E)$ vaut 1 en dessous de $E_F$ et 0 au dessus : \begin{equation} f_d(E) = \left\{\begin{matrix} 1 & \mbox{ si } & E \leq E_F \\ 0 & \mbox{ si } & E > E_F \end{matrix}\right. \end{equation} Et donc : \begin{equation}\left\{\begin{matrix} n_d & = & \dfrac{ 4\pi g m^3 c^3}{h^3} \displaystyle\int_{1}^{u_F} u \sqrt{u^2-1} du\\ P_d & = & \dfrac{4\pi g m^4 c^5}{3h^3} \displaystyle\int_{1}^{u_F} (u^2-1)^{3/2} du \end{matrix}\right.\end{equation} On note $n_0 = \dfrac{ 4\pi g m^3 c^3}{h^3} $ et $P_0 = \dfrac{4\pi g m^4 c^5}{3h^3}$. Le régime dégénéré peut être résolu analytiquement : \begin{equation} \displaystyle\int_{1}^{u_F} u \sqrt{u^2-1} du = \dfrac{1}{2} \displaystyle\int_{0}^{u_F^2 - 1} \sqrt{t} dt = \dfrac{1}{3} \left (u_F^2 - 1\right )^{3/2} \end{equation} Et \begin{equation} \displaystyle\int_{1}^{u_F} (u^2-1)^{3/2} du = \displaystyle\int_{0}^{\cosh^{-1} u_F}\sinh^4{(t)} dt \\ = \dfrac{3}{8} \cosh^{-1} u_F - \dfrac{1}{2} u_F \sqrt{u_F^2 - 1} + \dfrac{1}{8} u_F \sqrt{u_F^2 - 1} (2u_F^2 - 1) \end{equation} Ce qui donne, en définissant $x \equiv 3\dfrac{n}{n_0}$ : \begin{equation} P = P_0 \left [ \dfrac{3}{8} \sinh^{-1}{\left (x^{1/3} \right )} + \sqrt{1+ x^{2/3}} \left ( \dfrac{1}{4}x- \dfrac{3}{8} x^{1/3} \right ) \right ] \end{equation} Similairement on peut montrer que la densité d'énergie peut s'écrire : \begin{equation} \rho_e =\dfrac{3}{8} P_0 \left [ \sinh^{-1}{\left (x^{1/3} \right )} + \sqrt{1+ x^{2/3}} \left ( 2x- x^{1/3} \right ) \right ] \end{equation} Les courbes $n/n_0 \mapsto P/P_0$ sont calculées numériquement (facteurs dimensionnés exclus). On trouve

On observe pour un gaz dégénéré deux régimes différents :

• Faible densité : $P \sim P_0 \left ( \dfrac{n}{n_0} \right )^{5/3}$ (courbe en pointillés)
• Haute densité : $P \sim P_0 \left ( \dfrac{n}{n_0} \right )^{4/3}$ (courbe en traits discontinus)

Un gaz dicté par les effets thermiques se comporte comme un gaz dégénéré à forte densité et comme un gaz parfait à basse densité. (La relation pression/densité pour fermi dirac est une droite,

Résistance à la gravité

Dans une naine blanche, la force qui compense la pression de dégénérescence des électrons est la gravité. On peut montrer à partir de la relativité générale que l'équilibre se traduit par l'équation de Tolman-Oppenheimer :

\begin{equation} \left( 1 - \frac{2 G M(r)}{c^2 r} \right) P'(r) = - \frac{G}{r^2}\dfrac{1}{c^2} \left( \rho_m(r) + \rho_e(r) + P(r) \right) \left(M(r) + 4 \pi r^3 \frac{P(r)}{c^2} \right) \end{equation} $P$ est la pression, $\rho_m$ la densité d'énergie de masse de la matière baryonique (qui constitue l'essentiel de la masse d'une étoile), et $\rho_e$ celle du gaz d'électrons. $M(r)$ est la masse comprise dans la sphère de rayon $r$ centrée au coeur de l'étoile. La pression qui domine est celle de dégénérescence donc $P$ est la pression du gaz d'électrons. Par ailleurs la masse est reliée à la densité de matière et d'énergie par : et \begin{equation} M'(r) = 4\pi r^2 \dfrac{\rho_m(r) + \rho_e(r)}{c^2} \end{equation} On peut écrire $\rho_m \simeq n_b m_p c^2 $. où on définit le rapport entre densité baryonique et d'électron $\mu \equiv n_b / n_e$. Alors on a $n_e = \rho_m / (\mu m_p c^2)$. En définissant $\rho_0 \equiv n_0 m_p c^2$, il vient que $x = 3 \rho_m / (\mu \rho_0)$. Les naines blanches étant principalement constituées d'éléments tels que le carbone, il y a en moyenne un proton et un neutron pour chaque électron donc $\mu = 2$ On définit les variables adimensionnées associées : $p \equiv P/P_0$, $\epsilon = \rho_e/\rho_0$, $\xi = r/R_{\odot}$ et $m = M/M_{\odot}$ L'équation devient : \begin{equation} \left( 1 - \frac{2 G M_{\odot} m(\xi)}{c^2 R_{\odot} \xi} \right) \dfrac{P_0R_{\odot}^2 }{G R_{\odot}}p'(\xi) = - \frac{1}{\xi^2 c^2} \left( \rho_0 \mu x/ 3 + \rho_0 \epsilon + P_0 p(\xi) \right) \left(M_{\odot} m(\xi) + 4 \pi R_{\odot}^3 \xi^3 \frac{P_0 p(\xi)}{c^2} \right) \end{equation} En définissant les variables adimensionnées $\alpha \equiv \dfrac{P_0}{\rho_0} = \dfrac{m_e}{3 m_p}$ et $\beta = \dfrac{\rho_0 R_{\odot}^3}{M_{\odot}c^2} = \dfrac{ 4\pi g m_e^3 m_H c^3}{h^3} \dfrac{R_{\odot}^3}{M_{\odot}}$ ainsi que le rayon de schwarszchild du Soleil $r_s = 2GM_{\odot}/c^2$ alors : ^[?] \begin{equation} 2 \alpha \dfrac{R_{\odot}}{r_s} \left( 1 - \frac{r_s m(\xi)}{R_{\odot} \xi} \right) p'(\xi) = - \frac{1}{\xi^2} \left( \mu x (\xi) /3 + \epsilon(\xi) + \alpha p(\xi) \right) \left( m(\xi) + 4 \alpha \beta \pi \xi^3 p(\xi) \right) \end{equation} Et par ailleurs : \begin{equation} m'(\xi) = 4\pi \xi^2 \dfrac{\rho(\xi)}{\rho_0} = \dfrac{4}{3} \pi\xi^2 \dfrac{\rho_0 R_{\odot}^3}{M_{\odot}}(\mu x + 3\epsilon ) \end{equation} On peut aussi employer l'équation hydrostatique non relativiste : \begin{equation} 2 \alpha \dfrac{R_{\odot}}{r_s}p'(\xi) = -\dfrac{\mu m(\xi) x(\xi)}{3 \xi^2} \end{equation}

Résultat

Les équations d'équilibre sont résolues (Relativité générale ou gravitation newtonienne) et conduisent au résultat suivant :

Effondrement et supernova

On estime que le mécanisme d'effondrement d'une naine blanche donnant lieu a une supernova de type Ia est le suivant : (F. Hoyle, William A. Fowler  1960)

1. La naine blanche accrète de la matière en général d'une étoile compagnon telle qu'une géante rouge. Sa masse augmente jusqu'à devenir suffisamment proche de la limite de Chandrasekhar. Celle-ci devient alors instable (la pression de dégénerescence ne permet plus de contrer la gravité).

Emploi comme chandelles standards

De façon empirique, on sait au début des années 1990 que les supernovae de type Ia ont une magnitude maximale similaire, et des courbes de luminosité ($t\mapsto L(t)$) semblables. Ces courbes montrent toute une augmentation rapide jusqu'à l'atteinte d'une maximum puis une diminution plus lente.

De là, elles possèdent un certain potentiel en tant que chandelles standard. Une bonne chandelle standard doit avoir une dispersion en magnitude $\Delta M$ faible, pour que la méthode soit précise. Les céphéides variables par exemple, peuvent avoir des magnitudes absolues très différentes, mais celle-ci est fortement corrélée avec leur période - qui est facilement mesurable - si bien qu'on peut déduire leur magnitude intrinsèque avec une dispersion $\Delta M_{V} \sim $ 0,1 (L. N. Berdnikov, A. K. Dambis et al.  1997) . En 1993, Phillips montre à partir de mesures effectuées sur 9 SNe Ia proches (M. M. Phillips  1993) que celles-ci possèdent une dispersion en magnitude maximale intrinsèque de l'ordre de $\pm 0,6$ dans la bande V, et $\pm 0,8$ dans la bande B. Il cite notamment le cas de la supernova SN 1991bg qui est significativement moins lumineuses que les autres. Il note aussi que sa courbe de luminosité dans la bande B au cours du temps semble décroître plus rapidement. Des corrélations sont alors recherchées afin de déterminer si l'estimation de la luminosité maximale peut être affinée à l'aide d'autres observables. Dans la poursuite de l'idée des travaux de Pskovskii en 1984, Phillips teste l'hypothèse d'une corrélation entre rapidité du déclin de la luminosité des supernovae Ia et leur luminosité maximale. Il définit dans ce but un paramètre de déclin noté $\Delta m_{15}(B)$ qui correspond à la variation de magnitude apparente entre le pic de luminosité et 15 jours plus tard. Par la suite cette méthode est encore améliorée, à l'aide de templates ou de remises à l'échelle appliquées aux courbes de lumière (G. Goldhaber, D. E. Groom et al.  2001) . (Adam G. Riess, Alexei V. Filippenko et al.  1998) (S. Perlmutter, G. Aldering et al.  1999)