Momentanément oubliée après le succès de la nucléosynthèse stellaire, la nucléosynthèse primordiale, c'est-à-dire la formation de noyaux ayant eu lieu durant le Big-Bang, a connu un grand regain d'intérêt après la découverte du fond diffus cosmologique. Non seulement celui-ci confirme que l'Univers était beaucoup plus chaud dans le passé, et probablement suffisamment pour que des réactions nucléaires aient eu lieu à grande échelle, mais en plus la mesure de sa température est une contrainte expérimentale supplémentaire utile pour mieux tester ces modèles.

Au début des années 1960, les travaux d'Alpher, Follin et Hermann, ainsi que ceux d'Hayashi, ont permis d'obtenir une bonne description de la physique de l'Univers pour une température de l'ordre de la centaine de MeV - au-delà, la physique des particules n'est alors pas encore assez bien connue pour obtenir une meilleure description. A ces températures, l'Univers était constitué de protons et de neutrons (les baryons), d'électrons, de photons, et de neutrinos et antineutrinos. Les réactions entre ces différents constituants étaient suffisantes pour les maintenant en équilibre thermodynamique, et donc une compréhension des phénomènes physiques antérieurs à $\sim$ 100 MeV n'est pas nécessaire. L'Univers est alors décrit par un nombre limité de paramètres, les "conditions initiales", comme le ratio baryons/photons ($=(n_p + n_n)/n_{\gamma}$).

Avec le refroidissement de l'Univers, certaines réactions maintenant l'équilibre thermique sont interrompues. Le ratio protons/neutrons est ainsi constant, et n'évolue plus que par la désintégration spontanée des neutrons d'un temps de demi-vie de l'ordre de la dizaine de minutes. Une fois la température abaissée au dixième de MeV, les réactions nucléaires deviennent prédominantes, c'est le début à proprement parler de la nucléosynthèse primordiale. Afin d'estimer les abondances d'éléments résultantes, il faut alors intégrer toutes les réactions nucléaires et leur sections-efficaces aux calculs. C'est ce travail qui a été repoussé pendant plusieurs années après les derniers apports de Fermi et Turkevich.

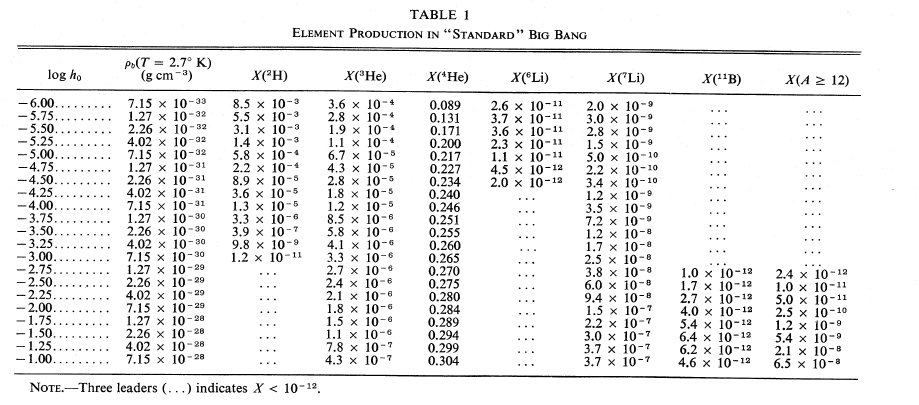
Après la découverte du fond diffus cosmologique, la donne change donc très vite. Le Big-Bang parait beaucoup plus vraisemblable et dont la nucléosynthèse primordiale aussi. Par ailleurs, l'abondance des éléments ${}^2_1\textrm{H}$ ${}^3_2\textrm{He}$, ${}^4_2\textrm{He}$ et ${}^{7}\textrm{Li}$, n'a pas encore d'explication satisfaisante, ce qui constitue une autre raison d'envisager des modes de production des éléments autre que la nucléosynthèse stellaire. En 1964, Hoyle et Tayler publient un article intitulé "The mystery of helium abundance" (F. HOYLE, R. J. TAYLER  1964) , dans lequel ils évaluent la vraisemblance d'une explication de l'abondance observée de l'hélium par une synthèse durant un Big-Bang chaud, donc via le mécanisme qu'Alpher et Hermann ont été les premiers à proposer. Ils soulignent, en plus de sa valeur trop élevée ($\textrm{He}/\textrm{H}\sim 0,01$) pour les mécanismes stellaires classiques de formation, l'homogénéité de l'abondance observée de l'hélium. Le fait que celle-ci dépende très peu de l'objet observé, et donc qu'elle soit similaire proche ou loin des sites de production stellaires, et insensible à leur âge, semble indiquer une origine différente. L'abondance observée est très grossièrement en accord avec une production d'origine cosmologique selon leurs calculs, qui prédisent $\textrm{He}/\textrm{H} \sim 0,14$ au minimum (une légère tension avec la valeur expérimentale un peu trop faible est tout de même observée). Ils concluent alors que l'hélium a du être produit à très haute température, comme cela est possible dans le cadre du Big-Bang chaud, ou bien dans des étoiles supermassives. D'autres études similaires sont menées en accord avec ce résultat. En 1967, Robert Wagoner, qui travaille à Caltech auprès de Fowler et Hoyle (B. Bertotti  1990) , publie les résultats d'une simulation impliquant 41 noyaux et 79 réactions faibles et nucléaires (Robert V. Wagoner, William A. Fowler et al.  1967) . Les sections efficaces de toutes ces réactions n'étant pas aisées à déterminer, certaines sont estimées à partir d'autres données (comme les énergies de liaison).

Les résultats indiquent un bon accord avec les observations d'abondance des éléments légers de l'époque pour une densité baryonique $\rho_b \simeq 2 \times 10^{-28} \textrm{kg}.\textrm{m}^{-3}$, ce qui est raisonnablement proche de la densité critique connue à l'époque ($\rho_c \simeq 10^{-26}\textrm{kg}.\textrm{m}^{-3}$). Fort de meilleures données nucléaires, Wagoner publie des résultats améliorés en 1973 (Robert V. Wagoner  1973) . Wagoner débute cet article en donnant 3 arguments en faveur de la nucléosynthèse primordiale :

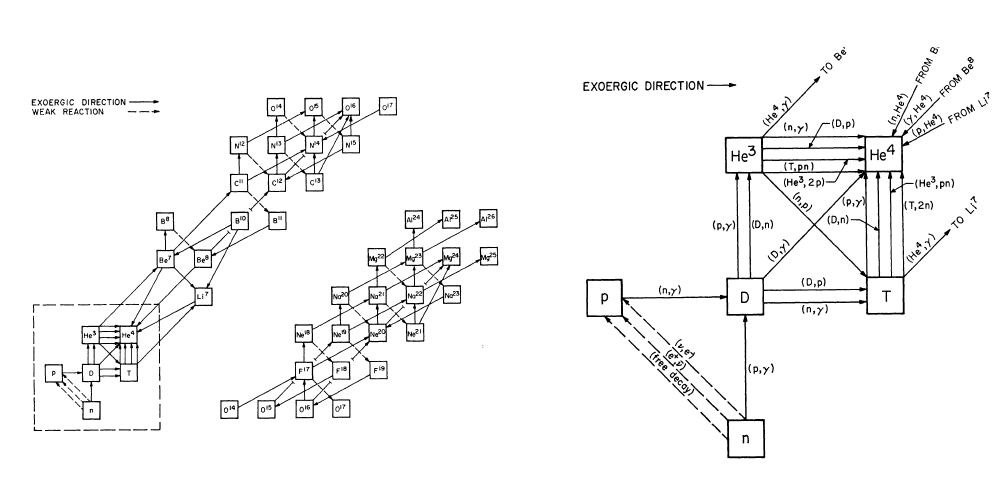
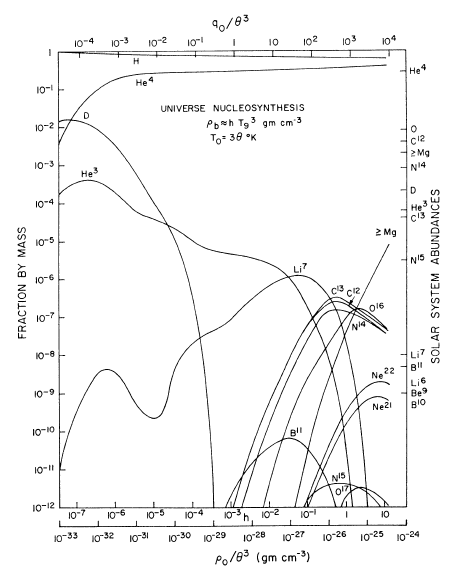
• La découverte de galaxies naines bleues jeunes (Bodo Baschek, Wallace L. W. Sargent et al.  1972) et pauvres en $\textrm{O}$ et $\textrm{Ne}$ mais avec une abondance en hélium similaire aux valeurs pour des objets plus anciens.
• Aucun processus astrophysique ne semble capable de produire autant d'hélium et de lithium qu'observé.
• L'isotropie constatée du fond de rayonnement désormais mesuré à 2,7$\pm$0,1 K et la nature de corps noir de son spectre sont des arguments très forts en faveur d'une interprétation comsologique.

Le tableau suivant résume la situation expérimentale en 1973 : Wagoner trouve par ailleurs les résultats suivants : L'accord avec les valeurs expérimentales est correct et permet de placer une limite supérieure sur la densité baryonique $\rho_b$. Celle-ci doit alors être inférieure à $\rho_b \simeq 7 \times 10^{-27} \textrm{kg}.\textrm{m}^{-3}$, insuffisant pour que $\rho_b = \rho_c$ (densité critique égale à la densité baryonique). Ainsi, d'après ces résultats, l'Univers ne peut-être plat s'il est constitué de matière baryonique seule.

La transformation de Lorentz est la transformation qui relie les coordonnées d'un évènements dans deux référentiels inertiels en mouvement rectiligne uniforme l'un par rapport à l'autre dans le cadre de la relativité restreinte. Elle découle naturellement de l'hypothèse selon laquelle un corps se déplaçant à la vitesse de la lumière $c$ dans un tel référentiel doit se déplacer à cette vitesse dans tous ces référentiels.

On se donne deux référentiels $\mathcal{R}$ et $\mathcal{R}'$ partageant la même origine à $t=0$, de mêmes axes, et tels que $\mathcal{R}'$ s'éloigne de $\mathcal{R}$ dans la direction $x$ à vitesse constante $v$. Si $(t,x,y,z)$ sont les coordonnées d'un évènement $A$ dans $\mathcal{R}$, et $(t',x',y',z')$ ses coordonnées dans $\mathcal{R}'$, alors : \begin{equation}\left\{\begin{matrix} ct' & = & \gamma (ct-\beta x)\\ x' & = & \gamma (x-\beta ct)\\ y' & = & y\\ z' & = & z \end{matrix}\right.\end{equation} Où $\gamma = \dfrac{1}{\sqrt{1-v^2/c^2}}$ est le facteur de Lorentz et $\beta = v/c$ le nombre de Lorentz.

La notion de transformation de Lorentz se généralise à d'autres quantités que les coordonnées : on appelle Quadrivecteur tout vecteur dont les composantes sont changées par passage d'un référentiel inertiel à un autre selon la transformation de Lorentz. C'est le cas par exemple des quadrivecteurs vitesses et accélérations $dx^\mu/ds$ et $d^2x^\mu/ds^2$, du quadrivecteur énergie-impulsion $p^\mu = (E/c, -\vec{p})$, ou encore du quadrivecteur potentiel $A^\mu = (\phi/c, -\vec{A})$.

La transformation de Lorentz laisse invariante la pseudo-norme d'un quadrivecteur. C'est par exemple le cas de $dx_\mu dx^\mu = ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2$, l'intervalle infinitésimal d'espace temps. On peut construire d'autres invariants comme le produit scalaire de deux 4-vecteur $A_\mu B^\mu = A^t B^t - A^x B^x - A^y B^y - A^z B^z$.

La loi de transformation relativiste des vitesses se déduit directement de cette transformation. On suppose, sans perdre de généralité, la même définition des référentiels $\mathcal{R}$ et $\mathcal{R}'$ que celle précédemment donnée; on suppose de plus qu'un corps se déplace à la vitesse $\vec{u} = (u_x,u_y,u_z)$ dans $\mathcal{R}$ et on cherche sa vitesse $\vec{u}'$ dans $\mathcal{R}'$. On remarque que $u_i = dx_i/dt$ et $u_i' = dx_i'/dt'$. De là : \begin{equation}\left\{\begin{matrix} \dfrac{dx'}{dt'} & = & \dfrac{c\gamma (dx-\beta c dt)}{\gamma(c dt-\beta dx)} = \dfrac{c(u_x dt-\beta c dt)}{(c dt-\beta u_x dt)}\\ \dfrac{dy'}{dt'} & = & \dfrac{c dy}{(c dt-\beta dx)} = \dfrac{c u_y dt}{(c dt-\beta u_x dt)}\\ \dfrac{dz'}{dt'} & = & \dfrac{c dz}{(c dt-\beta dx)} = \dfrac{c u_z dt}{(c dt-\beta u_x dt)}\\ \end{matrix}\right.\end{equation} Ce qui donne : \begin{equation}\left\{\begin{matrix} u_x' & = & \dfrac{u_x-v}{1-v u_x/c^2}\\ u_y' & = & \dfrac{u_y}{\gamma (1-v u_x/ c^2 )}\\ u_z' & = & \dfrac{u_z}{\gamma (1-v u_x/ c^2 )}\\ \end{matrix}\right.\end{equation}