Modèle standard de la cosmologie : le modèle $\Lambda$CDM

L'expérience COBE qui a accompli ses objectifs a été un grand succès, mais il y a encore beaucoup de marge pour des expériences de meilleures précisions. Par ailleurs, les récents développements, comme la découverte de l'accélération de l'Univers, et la mise au point de théories inflationnaires, suggèrent un modèle cosmologique standard appelé modèle $\Lambda$CDM. Ce modèle suppose que l'Univers est aujourd'hui exclusivement constitué (à l'exception du rayonnement du fond diffus cosmologique) de matière froide ($P=0$) et d'énergie du vide (d'équation d'état $P = -\rho$), en proportions telles que l'Univers soit plat.

Paramètre	Notation	Description
Âge de l'Univers	$t_0$	Temps écoulé depuis la singularité du Big-Bang.
Paramètre de densité baryonique	$\Omega_b h^2$	Paramètre de densité de baryons (matière ordinaire), d'équation d'état $P=0$.
Paramètre de densité de matière noire	$\Omega_{dm} h^2$	Paramètre de densité de la matière noire, d'équation d'état $P=0$.
Amplitude des fluctuations primordiales de courbure	$\Delta R^2$	Amplitude des fluctutions primordiales de la courbure scalaire.
Indice spectral scalaire	$n_s$	Les fluctuations primordiales de densité sont définies comme $\delta(x) = (\rho(x)-\bar{\rho})/\bar{\rho}$. Les modèles d'inflation prédisent que leur composantes de fourier vérifient :\begin{equation}\langle \delta_k \delta_{k'} \rangle \propto \dfrac{2\pi}{k^3} \delta(k-k') \left(\dfrac{k}{k_0}\right)^{n_s - 1}\end{equation} Un indice $n_s$ égal à 1 signifie que les fluctuations ont un spectre identique à toute échelle ("scale invariance").
Épaisseur optique à la réionisation.	$\tau$	L'épaisseur optique fait référence au taux d'absorption des photons du CMB entre leur émission et un instant donné au cours de l'expansion. Ce taux d'absorption augmente avec la distance parcourue par les photons du fond diffus cosmologique et donc avec le temps. La valeur de l'épaisseur optique de réionisation renseigne donc sur l'instant où celle-ci est survenue. Ce paramètre affecte naturellement l'aspect du CMB, et est laissé libre dans le modèle.

Des expériences plus précises que COBE sont capables de comparer les données d'observations du fond diffus cosmologique et de les comparer aux résultats attendu pour un jeu de ces paramètres. Cela permet de les mesurer via ces observations, et bien sûr de vérifier la validité du modèle $\Lambda$CDM. C'est l'objectif de la mission WMAP.

L'expérience WMAP

En 2001, le satellite WMAP, pour une mission organisée par la NASA, (Wilkinson Microwave Anisotropy Probe) est lancé et mis sur obite au point de Lagrange L2, à environ 1,5 million de kilomètres de la Terre. Ce satellite utilise des radiomètres différentiels pour mesurer les différences d'intensité du flux électromagnétique entre deux directions angulaires sur 5 bandes de fréquences comprises entre 22 et 90 GHz. Ceux-ci réalisent des mesures dans deux directions de polarisation différentes. Le diamètre des réflecteurs employés est d'environ 1,5 m. L'appareil est capable de mesurer des différences de température à une précision de 20 $\mu K$ et avec une résolution angulaire comprise entre 0,2$^{\circ}$ et 1$^{\circ}$ selon la longueur d'onde observée. La prise de données dure 9 ans, jusqu'en 2010, et fournit les cartes de température du fond diffus cosmologique les plus précises alors. Une description très complète de l'expérience est disponible à l'adresse http://map.gsfc.nasa.gov/mission/.

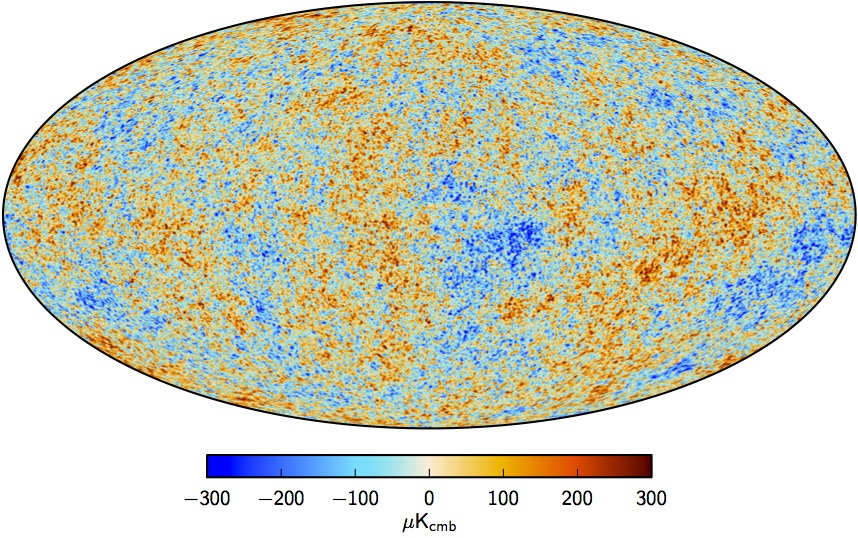
La carte finale est représentée sur la figure suivante

L'accord entre modèle et observation est plus que satisfaisant. Les mesures des paramètres cosmologiques fournies par WMAP sont par ailleurs les plus précises à ce jour. Les hypothèses de départ sont très bien vérifiées. En particulier, la platitude de l'Univers est confirmée à 0,4 % près (15 % avant WMAP!).

L'expérience Planck

L'expérience Planck, organisée par l'agence spatiale européenne, vise à confirmer les résultats de WMAP et améliorer encore leur précision. Lancé en 2009 à Kourou, le satellite Planck a collecté des données jusqu'en 2013, avec une extrême précision. Il est constitué de deux appareils de mesures principaux, le premier étant le Low Frequency Instrument mesurant l'intensité électromagnétique à des fréquences similaires à celles détectées par COBE et WMAP (30, 44 et 70 GHz) et un instrument haute fréquence (6 fréquences entre 100 et 857 GHz). Pour atteindre le degré de précision requis, certains appareils sont refroidis à une température de 0,1 K. La précision angulaire est comprise entre 0,1$^{\circ}$ et 0.5$^{\circ}$ selon la fréquence d'observation.

La mission est un grand succès et les résultats sont les plus précis à ce jour. Ils exploitent toute l'information cosmologique contenue dans le spectre de puissance du fond diffus cosmologique disponible à 'bas' multipôles (erreur systématique inférieure à la variance cosmique).

La transformation de Lorentz est la transformation qui relie les coordonnées d'un évènements dans deux référentiels inertiels en mouvement rectiligne uniforme l'un par rapport à l'autre dans le cadre de la relativité restreinte. Elle découle naturellement de l'hypothèse selon laquelle un corps se déplaçant à la vitesse de la lumière $c$ dans un tel référentiel doit se déplacer à cette vitesse dans tous ces référentiels.

On se donne deux référentiels $\mathcal{R}$ et $\mathcal{R}'$ partageant la même origine à $t=0$, de mêmes axes, et tels que $\mathcal{R}'$ s'éloigne de $\mathcal{R}$ dans la direction $x$ à vitesse constante $v$. Si $(t,x,y,z)$ sont les coordonnées d'un évènement $A$ dans $\mathcal{R}$, et $(t',x',y',z')$ ses coordonnées dans $\mathcal{R}'$, alors : \begin{equation}\left\{\begin{matrix} ct' & = & \gamma (ct-\beta x)\\ x' & = & \gamma (x-\beta ct)\\ y' & = & y\\ z' & = & z \end{matrix}\right.\end{equation} Où $\gamma = \dfrac{1}{\sqrt{1-v^2/c^2}}$ est le facteur de Lorentz et $\beta = v/c$ le nombre de Lorentz.

La notion de transformation de Lorentz se généralise à d'autres quantités que les coordonnées : on appelle Quadrivecteur tout vecteur dont les composantes sont changées par passage d'un référentiel inertiel à un autre selon la transformation de Lorentz. C'est le cas par exemple des quadrivecteurs vitesses et accélérations $dx^\mu/ds$ et $d^2x^\mu/ds^2$, du quadrivecteur énergie-impulsion $p^\mu = (E/c, -\vec{p})$, ou encore du quadrivecteur potentiel $A^\mu = (\phi/c, -\vec{A})$.

La transformation de Lorentz laisse invariante la pseudo-norme d'un quadrivecteur. C'est par exemple le cas de $dx_\mu dx^\mu = ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2$, l'intervalle infinitésimal d'espace temps. On peut construire d'autres invariants comme le produit scalaire de deux 4-vecteur $A_\mu B^\mu = A^t B^t - A^x B^x - A^y B^y - A^z B^z$.

La loi de transformation relativiste des vitesses se déduit directement de cette transformation. On suppose, sans perdre de généralité, la même définition des référentiels $\mathcal{R}$ et $\mathcal{R}'$ que celle précédemment donnée; on suppose de plus qu'un corps se déplace à la vitesse $\vec{u} = (u_x,u_y,u_z)$ dans $\mathcal{R}$ et on cherche sa vitesse $\vec{u}'$ dans $\mathcal{R}'$. On remarque que $u_i = dx_i/dt$ et $u_i' = dx_i'/dt'$. De là : \begin{equation}\left\{\begin{matrix} \dfrac{dx'}{dt'} & = & \dfrac{c\gamma (dx-\beta c dt)}{\gamma(c dt-\beta dx)} = \dfrac{c(u_x dt-\beta c dt)}{(c dt-\beta u_x dt)}\\ \dfrac{dy'}{dt'} & = & \dfrac{c dy}{(c dt-\beta dx)} = \dfrac{c u_y dt}{(c dt-\beta u_x dt)}\\ \dfrac{dz'}{dt'} & = & \dfrac{c dz}{(c dt-\beta dx)} = \dfrac{c u_z dt}{(c dt-\beta u_x dt)}\\ \end{matrix}\right.\end{equation} Ce qui donne : \begin{equation}\left\{\begin{matrix} u_x' & = & \dfrac{u_x-v}{1-v u_x/c^2}\\ u_y' & = & \dfrac{u_y}{\gamma (1-v u_x/ c^2 )}\\ u_z' & = & \dfrac{u_z}{\gamma (1-v u_x/ c^2 )}\\ \end{matrix}\right.\end{equation}